已知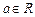 ,函数
,函数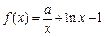 ,
,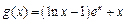 (其中
(其中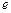 为自然对数的底数).(1)判断函数
为自然对数的底数).(1)判断函数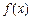 在区间
在区间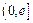 上的单调性;(2)是否存在实数
上的单调性;(2)是否存在实数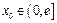 ,使曲线
,使曲线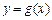 在点
在点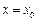 处的切线与
处的切线与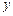 轴垂直? 若存在,求出
轴垂直? 若存在,求出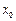 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本大题满分14分)
函数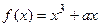 与
与 的图象有公共点
的图象有公共点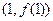 ,且它们的图象在该点处的切线相同。记
,且它们的图象在该点处的切线相同。记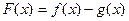 。
。
(Ⅰ)求 的表达式,并求
的表达式,并求 在
在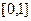 上的值域;
上的值域;
(Ⅱ)设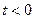 ,函数
,函数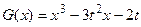 ,
,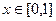 。若对于任意
。若对于任意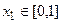 ,总存在
,总存在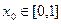 ,使得
,使得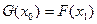 ,求实数
,求实数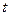 的取值范围。
的取值范围。
(本大题共13分)
已知函数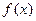 是定义在R的奇函数,当
是定义在R的奇函数,当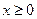 时,
时,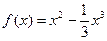 .
.
(1)求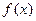 的表达式;
的表达式;
(2)讨论函数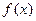 在区间
在区间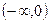 上的单调性;
上的单调性;
(3)设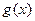 是函数
是函数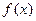 在区间
在区间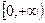 上的导函数,问是否存在实数
上的导函数,问是否存在实数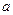 ,满足
,满足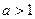 并且使
并且使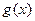 在区间
在区间 上的值域为
上的值域为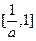 ,若存在,求出
,若存在,求出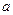 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
(本大题满分12分)
设 为实常数,函数
为实常数,函数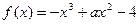 ,
,
⑴若函数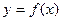 的图象在点
的图象在点 处的切线的倾斜角为
处的切线的倾斜角为 ,求函数
,求函数 的单调区间;
的单调区间;
⑵若存在 ,使
,使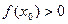 ,求
,求 的取值范围。
的取值范围。
(本大题满分12分)用半径为 圆铁皮剪出一个圆心角为
圆铁皮剪出一个圆心角为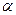 的扇形,制成一个圆锥形容器,扇形的圆心角
的扇形,制成一个圆锥形容器,扇形的圆心角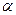 多大时,容器的容积最大?
多大时,容器的容积最大?
 |
(本大题满分12分)已知集合 ,
, ,
,
若 ,求实数
,求实数 的取值范围。
的取值范围。