(本题满分12分.)已知26列货车以相同的速度v由A地驶向相距400千米远的B地,
每两列货车间的距离为d千米,现知d与v速度的平方成正比,且当v=20,d=1.
(1) 写出d关于v的函数解析式式及定义域;
(2)若不计货车的长度,则26列货车都到达B地至少需要多少小时?此时货车速度为多少?
已知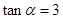 ,计算:
,计算:
(1)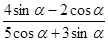
(2)
(3)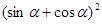
(本小题满分10分)选修4-5:不等式选讲.
设函数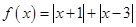 .
.
(1)求不等式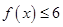 的解集;
的解集;
(2)若存在 使得
使得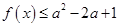 成立,求实数
成立,求实数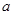 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系和参数方程.
已知圆 :
: (
( 为参数),直线
为参数),直线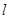 :
: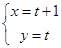 (为参数),.
(为参数),.
(1)若以原点为极点,以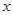 轴正半轴为极轴建立极坐标系,求出直线
轴正半轴为极轴建立极坐标系,求出直线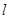 的极坐标方程;
的极坐标方程;
(2)试判断直线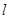 与圆
与圆 的位置关系,并说明理由,若相交,求出其相交弦长.
的位置关系,并说明理由,若相交,求出其相交弦长.
(本小题满分10分)选修4-1:几何证明选讲.
如下图所示,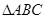 内接于圆
内接于圆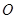 ,
,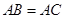 ,直线
,直线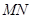 切圆
切圆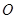 于点
于点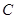 ,
,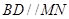 ,
,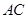 与
与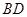 相交于点
相交于点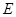 .求证:
.求证: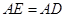 .
.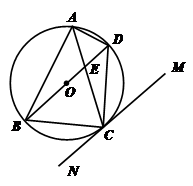
(本小题满分12分)已知椭圆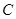 :
: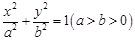 的右焦点
的右焦点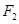 和上顶点
和上顶点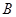 在直线
在直线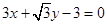 上,
上, 、
、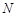 为椭圆
为椭圆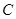 上不同两点,且满足
上不同两点,且满足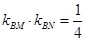 .
.
(1)求椭圆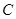 的标准方程;
的标准方程;
(2)证明:直线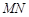 恒过定点
恒过定点 .
.