函数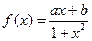 是定义在
是定义在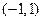 上的奇函数,且
上的奇函数,且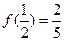 ,
,
(1)确定函数 的解析式;
的解析式;
(2)判断 在
在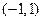 上的单调性并用定义证明.
上的单调性并用定义证明.
(3)解不等式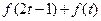 <0;
<0;
已知双曲线 的离心率e=2,且
的离心率e=2,且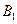 、
、 分别是双曲线虚轴的上、下端点
分别是双曲线虚轴的上、下端点
(Ⅰ)若双曲线过点 (
(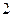 ,
,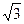 ),求双曲线的方程;
),求双曲线的方程;
(Ⅱ)在(Ⅰ)的条件下,若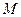 、
、 是双曲线上不同的两点,且
是双曲线上不同的两点,且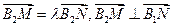 ,求直线
,求直线 的方程
的方程
椭圆C的中心为坐标原点O,焦点在y轴上,离心率e = ,椭圆上的点到焦点的最短距离为1-e, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且 .
.
(1)求椭圆方程;
(2)若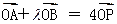 ,求m的取值范围.
,求m的取值范围.
已知双曲线的中心在原点,焦点F1、F2在坐标轴上,离心率为且过点(4,-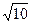 )
)
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)求△F1MF2的面积.
已知圆 :
: .
.
(1)直线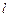 过点
过点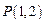 ,且与圆
,且与圆 交于
交于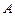 、
、 两点,若
两点,若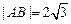 ,求直线
,求直线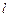 的方程;
的方程;
(2)过圆 上一动点
上一动点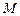 作平行于
作平行于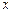 轴的直线
轴的直线 ,设
,设 与
与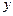 轴的交点为
轴的交点为 ,若向量
,若向量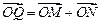 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
已知方向向量为 的直线
的直线 过椭圆C:=1(a>b>0)的焦点以及点(0,
过椭圆C:=1(a>b>0)的焦点以及点(0,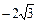 ),椭圆C的中心关于直线
),椭圆C的中心关于直线 的对称点在椭圆C的右准线上。
的对称点在椭圆C的右准线上。
⑴求椭圆C的方程。
⑵过点E(-2,0)的直线 交椭圆C于点M、N,且满足
交椭圆C于点M、N,且满足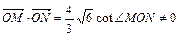 ,(O为坐标原点),求直线
,(O为坐标原点),求直线 的方程。
的方程。