(本小题满分12分)在锐角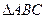 中 ,三个内角A、B、C的对边分别为a、b、c,且满足
中 ,三个内角A、B、C的对边分别为a、b、c,且满足
(1)求 的值;
的值;
(2)若b=3,求a+c的最大值。
设函数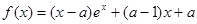 ,
, 。
。
(1)当 时,求
时,求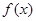 的单调区间;
的单调区间;
(2)(i)设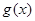 是
是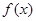 的导函数,证明:当
的导函数,证明:当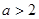 时,在
时,在 上恰有一个
上恰有一个 使得
使得 ;
;
(ii)求实数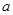 的取值范围,使得对任意的
的取值范围,使得对任意的 ,恒有
,恒有 成立。
成立。
注: 为自然对数的底数。
为自然对数的底数。
某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售高订购,决定当一次订量超过100个时,每多订购一个,订购的全部零件的出厂单价降低0.02元,但实际出厂单价不能低于51元.
(1)当一次订购量为多少个时,零件的实际出厂单价恰好降为51元?
(2)设一次订购量为x个,零件的实际出厂单价为P元,写出函数P=f(x)的表达式.
(3)当销售商一次订购500个零件时,该厂获得的利润是多少元?如果订购1 000个,利润又是多少元(工厂售出一个零件的利润=实际出厂单价-成本价)?
如图,在四棱锥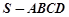 中,底面
中,底面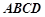 是直角梯形,
是直角梯形, ∥
∥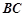 ,
, ,
,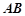 ⊥平面SAD,点
⊥平面SAD,点 是
是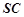 的中点,且
的中点,且 ,
,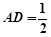 .
. 
(1)求四棱锥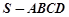 的体积;
的体积;
(2)求证: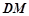 ∥平面
∥平面 ;
;
(3)求直线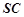 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.
在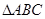 中,角
中,角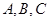 所对的边分别为
所对的边分别为 ,且满足
,且满足 ,
,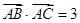 .
.
(1)求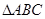 的面积;(2)若
的面积;(2)若 ,求
,求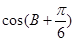 的值。
的值。
已知等差数列 的前
的前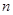 项和为
项和为 ,且
,且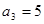 ,
, .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设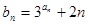 ,求数列
,求数列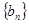 的前
的前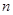 项和
项和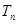 .
.