如图,在四棱锥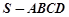 中,底面
中,底面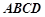 是直角梯形,
是直角梯形, ∥
∥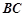 ,
, ,
,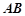 ⊥平面SAD,点
⊥平面SAD,点 是
是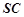 的中点,且
的中点,且 ,
,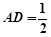 .
. 
(1)求四棱锥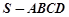 的体积;
的体积;
(2)求证: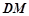 ∥平面
∥平面 ;
;
(3)求直线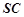 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.
(本小题满分16分)已知函数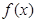 =
=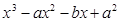 ,
,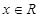 ,
,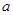 ,
,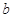 为常数。
为常数。
(1)若函数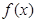 在
在 =1处有极值10,求实数
=1处有极值10,求实数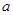 ,
,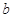 的值;
的值;
(2)若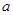 =0,(I)方程
=0,(I)方程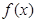 =2在
=2在 ∈[-4,4]上恰有3个不相等的实数解,求实数
∈[-4,4]上恰有3个不相等的实数解,求实数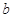 的取值范围;(II)不等式
的取值范围;(II)不等式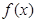 +2
+2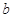 ≥0对
≥0对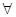
 ∈[1,4]恒成立,求实数
∈[1,4]恒成立,求实数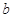 的取值范围。
的取值范围。
(本小题满分16分) 已知圆 的方程为
的方程为 ,直线
,直线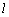 的方程为
的方程为 ,点
,点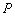 在直线
在直线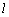 上,过
上,过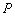 点作圆
点作圆 的切线
的切线 ,切点为
,切点为 .
.
(1)若 ,试求点
,试求点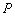 的坐标;
的坐标;
(2)若 点的坐标为
点的坐标为 ,过
,过 作直线与圆
作直线与圆 交于
交于 两点,当
两点,当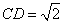 时,求直线
时,求直线 的方程
的方程
(3)经过 三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。
三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。
(本小题满分16分)某地有三个村庄,分别位于等腰直角三角形ABC的三个顶点处,已知AB=AC=18km,现计划在BC边的高AO上一点P处建造一个变电站. 记P到三个村庄的距离之和为y ,(1)设 ,把y表示成
,把y表示成 的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
的函数关系式;(2)变电站建于何处时,它到三个小区的距离之和最小?
(本小题满分14分)已知椭圆C的中心O在原点,长轴在x轴上,焦距为 ,短轴长为8,
,短轴长为8,
(1)求椭圆C的方程;
(2)过点 作倾斜角为
作倾斜角为 的直线交椭圆C于A、B两点,求
的直线交椭圆C于A、B两点,求 的面积。
的面积。
(本小题满分14分)如图,长方体ABCD—A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
(1)求证:直线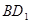 ∥平面
∥平面 ;
;
(2)求证:平面
 平面
平面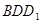 ;
;
(3)求三棱锥D—PAC的体积。