已知函数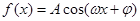 (
(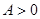 ,
,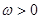 ,
,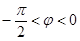 )的图像与
)的图像与 轴的交点为
轴的交点为 ,它在
,它在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为 和
和

(1)求函数 的解析式;
的解析式;
(2)若锐角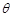 满足
满足 ,求
,求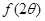 的值.
的值.
已知函数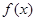 的定义域是
的定义域是 ,
, 是
是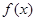 的导函数,且
的导函数,且 在
在 内恒成立.
内恒成立.
(1)求函数 的单调区间;
的单调区间;
(2)若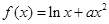 ,求
,求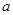 的取值范围;
的取值范围;
(3)设 是
是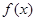 的零点,
的零点, ,求证:
,求证:
国家助学贷款是由财政贴息的信用贷款(即无利息贷款),旨在帮助高校家庭经济困难学生支付在校学习期间所需的学费、住宿费及生活费.每一年度申请总额不超过6000元.某大学2013届毕业生小王在本科期间共申请了24000元助学贷款,并承诺在毕业后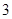 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加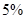 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多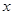 元.
元.
(1)假设小王在第 个月还清贷款(
个月还清贷款(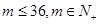 ),试用
),试用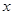 和
和 表示小王第
表示小王第 (
( )个月的还款额
)个月的还款额 ;
;
(2)当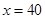 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款?
(3)在(2)的条件下,他还清最后一笔贷款的那个月的工资的余额是否能满足此月 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: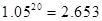 )
)
如图,正方形 所在的平面与正方形
所在的平面与正方形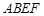 所在的平面相垂直,
所在的平面相垂直, 、
、 分别是
分别是 、
、 的中点.
的中点.
(1)求证:面 面
面 ;
;
(2)求直线 与平面
与平面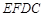 所成的角正弦值.
所成的角正弦值.
甲、乙两人用农药治虫,由于计算错误,在A、B两个喷雾器中分别配制成12%和6%的药水各10千克,实际要求两个喷雾器中的农药的浓度是一样的,现在只有两个容量为1千克的药瓶,他们从A、B两个喷雾器中分别取1千克的药水,将A中取得的倒入B中,B中取得的倒入A中,这样操作进行了n次后,A喷雾器中药水的浓度为 ,B喷雾器中药水的浓度为
,B喷雾器中药水的浓度为 .
.
(1)证明: 是一个常数;
是一个常数;
(2)求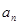 与
与 的关系式;
的关系式;
(3)求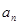 的表达式.
的表达式.