(本小题满分14分)如图,四棱锥 中,
中,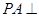 平面
平面 ,底面
,底面 是直角梯形,
是直角梯形, //
//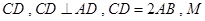 为
为 中点.
中点.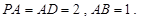
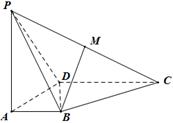
(Ⅰ)求证: //平面
//平面 ;
;
(Ⅱ)在侧面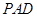 内找一点
内找一点 ,使
,使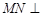 平面
平面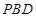 ;
;
(Ⅲ)求直线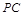 与平面
与平面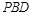 所成角的正弦值.
所成角的正弦值.
已知集合A={x|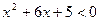 },B={x|−1≤x<1},
},B={x|−1≤x<1},
(1)求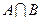 ;(2)若全集U=
;(2)若全集U=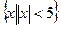 ,求CU(A∪B);
,求CU(A∪B);
(3)若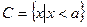 ,且
,且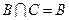 ,求
,求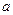 的取值范围.
的取值范围.
已知:函数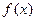 对一切实数
对一切实数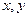 都有
都有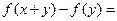
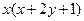 成立,且
成立,且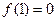 .
.
(1)求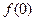 的值。
的值。
(2)求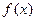 的解析式。
的解析式。
(3)已知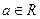 ,设P:当
,设P:当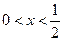 时,不等式
时,不等式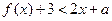 恒成立;Q:当
恒成立;Q:当 时,
时,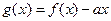 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的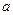 的集合记为
的集合记为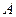 ,满足Q成立的
,满足Q成立的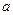 的集合记为
的集合记为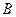 ,求
,求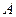 ∩
∩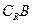 (
(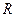 为全集)。
为全集)。
已知 是定义在R上的偶函数,当
是定义在R上的偶函数,当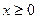 时,
时,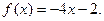
(1)写出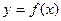 的解析式;
的解析式;
(2)画出函数的 图像;
图像;
(3)写出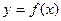 在
在 上的值域
上的值域 。
。
某自来水厂的蓄水池中有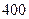 吨水,每天零点开始向居民供水,同时以每小时
吨水,每天零点开始向居民供水,同时以每小时 吨的速度向池中注水.已知
吨的速度向池中注水.已知 小时内向居民供水总量为
小时内向居民供水总量为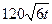 吨
吨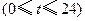 ,问
,问
(1)每天几点时蓄水池中的存水量最少?
(2)若池中存水量不多于 吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
吨时,就会出现供水紧张现象,则每天会有几个小时出现这种现象?
已知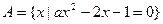 ,如果
,如果 ,求
,求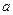 的取值
的取值