已知函数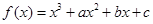 在
在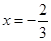 与
与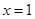 时都取得极值.
时都取得极值.
(1)求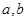 的值与函数
的值与函数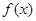 的单调区间
的单调区间
(2)若对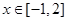 ,不等式
,不等式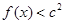 恒成立,求
恒成立,求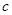 的取值范围.
的取值范围.
如图,直线 平面
平面 ,
, 为正方形,
为正方形, ,求直线
,求直线 与
与 所成角的大小.
所成角的大小.
已知函数 ,函数
,函数 .
.
(1)若 ,求不等式
,求不等式 的解集;
的解集;
(2)若对任意 ,均存在
,均存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知椭圆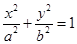 的左焦点
的左焦点 为圆
为圆 的圆心,且椭圆上的点到点
的圆心,且椭圆上的点到点 的距离的最小值为
的距离的最小值为 .
.
(1)求椭圆的方程;
(2)已知经过点 的动直线
的动直线 与椭圆交于不同的两点
与椭圆交于不同的两点 ,点
,点 ,求
,求 的值.
的值.
已知圆 过
过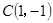 ,
, 两点,且圆心
两点,且圆心 在
在 上.
上.
(1)求圆 的方程;
的方程;
(2)设点 是直线
是直线 上的动点,
上的动点,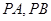 是圆
是圆 的两条切线,
的两条切线, 为切点,求四边形
为切点,求四边形 面积的最小值.
面积的最小值.
某日用品按行业质量标准分成五个等级,等级系数依次为1,2,3,4,5.现从一批日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如表所示:
(1)求 的值;
的值;
(2)从等级为4的2件日用品和等级为5的3件日用品中任取两件(假定每件日用品被取出的可能性相同),求这两件日用品的等级系数恰好相等的概率.