某游泳馆出售学生游泳卡,每张240元,使用规定:不记名,每卡每次只限1人,每天只限1次,某班有48名学生,老师打算组织同学们去游泳,除需购买若干张游泳卡外,每次还要包一辆汽车,无论乘坐多少人,每次的 包车费均为40元,若使每个同学游8次,每人最少交多少钱?
包车费均为40元,若使每个同学游8次,每人最少交多少钱?
如图,正方形 所在平面与平面四边形
所在平面与平面四边形 所在平面互相垂直,△
所在平面互相垂直,△ 是等腰直角三角形,
是等腰直角三角形,

(1)线段 的中点为
的中点为 ,线段
,线段 的中点为
的中点为 ,求证:
,求证: ;
;
(2)求直线 与平面
与平面 所成角的正切值.
所成角的正切值.
已知在等比数列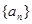 中,
中, ,且
,且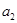 是
是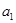 和
和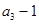 的等差中项.
的等差中项.
(1)求数列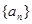 的通项公式;
的通项公式;
(2)若数列 满足
满足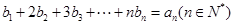 ,求
,求 的通项公式
的通项公式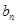 .
.
已知函数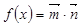 ,其中
,其中 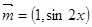 ,
,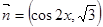 ,在
,在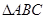 中,
中,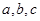 分别是角
分别是角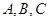 的对边,且
的对边,且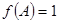 ,
,
(1)求角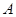 ;(2)若
;(2)若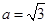 ,
, ,求
,求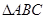 的面积.
的面积.
已知函数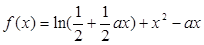
 为常数,
为常数,
(1)当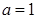 时,求函数
时,求函数 在
在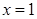 处的切线方程;
处的切线方程;
(2)当 在
在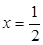 处取得极值时,若关于
处取得极值时,若关于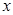 的方程
的方程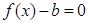 在
在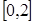 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数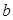 的取值范围;
的取值范围;
(3)若对任意的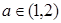 ,总存在
,总存在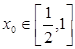 ,使不等式
,使不等式 成立,求实数
成立,求实数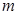 的取值范围。
的取值范围。
椭圆 :
: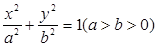 的右焦点
的右焦点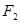 与抛物线
与抛物线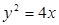 的焦点重合,过
的焦点重合,过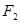 作与
作与 轴垂直的直线
轴垂直的直线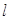 与椭圆交于
与椭圆交于 两点,与抛物线交于
两点,与抛物线交于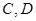 两点,且
两点,且 。
。
(1)求椭圆 的方程;
的方程;
(2)若过点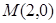 的直线与椭圆
的直线与椭圆 相交于两点
相交于两点 ,设
,设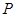 为椭圆
为椭圆 上一点,且满足
上一点,且满足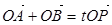
 为坐标原点),当
为坐标原点),当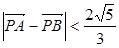 时,求实数
时,求实数 的取值范围。
的取值范围。