已知函数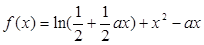
 为常数,
为常数,
(1)当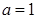 时,求函数
时,求函数 在
在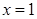 处的切线方程;
处的切线方程;
(2)当 在
在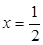 处取得极值时,若关于
处取得极值时,若关于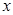 的方程
的方程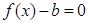 在
在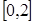 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数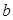 的取值范围;
的取值范围;
(3)若对任意的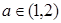 ,总存在
,总存在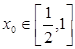 ,使不等式
,使不等式 成立,求实数
成立,求实数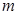 的取值范围。
的取值范围。
已知等比数列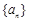 的首项
的首项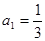 ,前n项和为
,前n项和为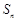 ,满足
,满足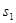 、2
、2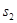 、
、
 成等差数列;
成等差数列;
(Ⅰ)求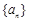 的通项公式;
的通项公式;
(Ⅱ)设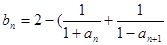 ),数列
),数列 的前n项和为Tn ,求证:
的前n项和为Tn ,求证: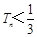 .
.
若二次函数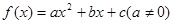 ,满足
,满足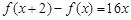 且
且 =2.
=2.
(Ⅰ)求函数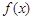 的解析式;
的解析式;
(Ⅱ)若存在 ,使不等式
,使不等式 成立,求实数m的取值范围.
成立,求实数m的取值范围.
如图,在四棱锥P—ABCD中,底面ABCD是正方形,PD⊥底面ABCD,M,N分别是PA,BC的中点,且PD=AD=1.
(Ⅰ)求证:MN∥平面PCD;
(Ⅱ)求证:平面PAC⊥平面PBD.
已知函数 sin(ωx+φ)(ω>0,0≤φ≤π)为偶函数,其图象上相邻的两个最低点间的距离为2π.
sin(ωx+φ)(ω>0,0≤φ≤π)为偶函数,其图象上相邻的两个最低点间的距离为2π.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若将函数 图像向右平移
图像向右平移 个单位得到函数
个单位得到函数 的图像,若
的图像,若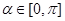 ,且
,且 ,求α的值.
,求α的值.
(本小题满分15分)如图,已知抛物线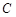 :
: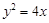 ,过焦点
,过焦点 斜率大于零的直线
斜率大于零的直线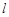 交抛物线于
交抛物线于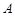 、
、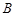 两点,且与其准线交于点
两点,且与其准线交于点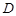 .
.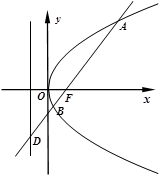
(Ⅰ)若线段 的长为
的长为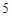 ,求直线
,求直线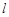 的方程;
的方程;
(Ⅱ)在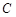 上是否存在点
上是否存在点 ,使得对任意直线
,使得对任意直线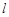 ,直线
,直线 ,
,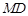 ,
,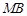 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.