设函数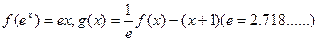
(1)求函数g(x)的极大值
(2)求证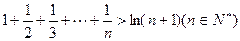
(3)若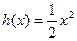 ,曲线y=
,曲线y=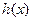 与 y=
与 y=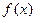 是否存在公共点,若存在公共点,在公共点处是否存在公切线,若存在,求出公切线方程,若不存在,说明理由。
是否存在公共点,若存在公共点,在公共点处是否存在公切线,若存在,求出公切线方程,若不存在,说明理由。
若下列方程: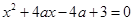 ,
,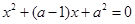 ,
,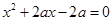 ,至少有一个方程有实根,试求实数
,至少有一个方程有实根,试求实数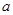 的取值范围.
的取值范围.
设函数 对任意
对任意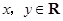 ,都有
,都有 且
且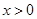 时,
时,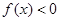 .
.
(Ⅰ)证明 为奇函数;
为奇函数;
(Ⅱ)证明 在
在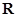 上为减函数.
上为减函数.
求证:以过抛物线 焦点的弦为直径的圆必与
焦点的弦为直径的圆必与 相切(用分析法证)
相切(用分析法证)
现调查中学生性别与肥胖的关系,从一学校随机抽取300人,得到以下的列联表:
| 肥胖 |
不肥胖 |
合计 |
|
| 男生 |
35 |
90 |
125 |
| 女生 |
35 |
140 |
175 |
| 合计 |
70 |
230 |
300 |
由表中数据计算得 ,中学生的性别是否与肥胖有关系?为什么?
,中学生的性别是否与肥胖有关系?为什么?
有研究者欲考查某一高考试题的得分情况是否存在性别差异,统计结果如下:
| 及格 |
不及格 |
合计 |
|
| 男生 |
290 |
160 |
450 |
| 女生 |
100 |
350 |
450 |
| 合计 |
390 |
510 |
900 |
该统计结果说明什么问题?