(本小题满分10分)如图,在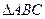 中,
中,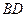 为AC边上的高,
为AC边上的高,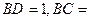
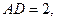 沿BD将
沿BD将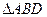 翻折,使得
翻折,使得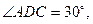 得到几何体
得到几何体
(I)求证:AC^平面BCD;
(Ⅱ)求异面直线AB与CD所成角的正切值.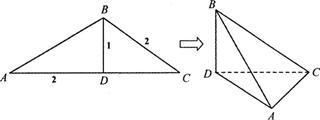
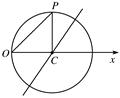
设直线l过点P(-3,3),且倾斜角为 .
.
(1)写出直线l的参数方程;
(2)设此直线与曲线C: (θ为参数)交于A,B两点,求|PA|·|PB|.
(θ为参数)交于A,B两点,求|PA|·|PB|.
在平面直角坐标系xOy中,直线l的参数方程为 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 (θ为参数).试求直线l和曲线C的普通方程,并求出它们的公共点的坐
(θ为参数).试求直线l和曲线C的普通方程,并求出它们的公共点的坐
已知在直角坐标系xOy中,曲线C的参数方程为 (θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin
(θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin  =2
=2 .
.
(1)求曲线C在极坐标系中的方程;
(2)求直线l被曲线C截得的弦长.
在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系.已知点A的极坐标为 ,直线l的极坐标方程为ρcos
,直线l的极坐标方程为ρcos =a,且点A在直线l上.
=a,且点A在直线l上.
(1)求a的值及直线l的直角坐标方程;
(2)圆C的参数方程为 (α为参数),试判断直线l与圆C的位置关系.
(α为参数),试判断直线l与圆C的位置关系.
在极坐标系中,已知圆C经过点P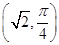 ,圆心为直线ρsin
,圆心为直线ρsin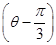 =-
=-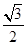 与极轴的交点,求圆C的极坐标方程.
与极轴的交点,求圆C的极坐标方程.