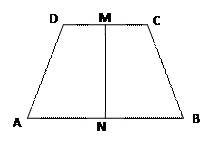
如图,四边形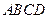 是一个梯形,
是一个梯形,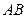 ∥
∥ ,且
,且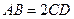 ,
,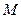 、
、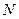 分别是
分别是 、
、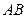 的中点,已知
的中点,已知 =
=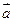 ,
, =
=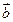 ,试用
,试用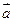 、
、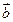 分别表示
分别表示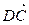 、
、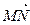 。
。
已知函数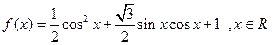 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在
在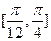 上的最大值和最小值,并求函数取得最大值和最小值时的自变量
上的最大值和最小值,并求函数取得最大值和最小值时的自变量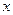 的值.
的值.
已知向量 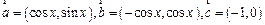 .
.
(1)若  ,求向量
,求向量  的夹角;
的夹角;
(2)已知  ,且
,且 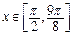 ,当
,当 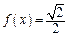 时,求 x的值并求
时,求 x的值并求 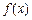 的值域.
的值域.
已知向量 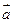 与
与 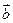 的夹角为60°,
的夹角为60°, 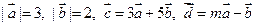 。
。
(1)求 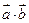 的值;(2)若
的值;(2)若  ,求实数
,求实数  的值。
的值。 
已知平面内两定点 ,动点
,动点 满足条件:
满足条件: ,设点
,设点 的轨迹是曲线
的轨迹是曲线 为坐标原点。
为坐标原点。
(I)求曲线 的方程;
的方程;
(II)若直线 与曲线
与曲线 相交于两不同点
相交于两不同点 ,求
,求 的取值范围;
的取值范围;
(III)(文科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,记
,记 分别为
分别为 两点的横坐标,求
两点的横坐标,求 的最小值。
的最小值。
(理科做)设 两点分别在直线
两点分别在直线 上,若
上,若 ,求
,求 面积的最大值。
面积的最大值。