给定函数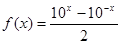
(1)求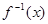 ;
;
(2)判断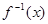 的奇偶性,并证明你的结论。
的奇偶性,并证明你的结论。
(本小题满分12分)设函数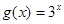 ,
,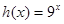 .
.
(1)解方程: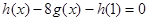 ;
;
(2)令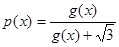 ,求证:
,求证: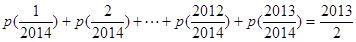 ;
;
(3)若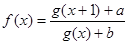 是实数集
是实数集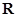 上的奇函数,且
上的奇函数,且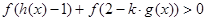 对任意实数
对任意实数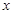 恒成立,求实数
恒成立,求实数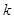 的取值范围.
的取值范围.
(参考公式:当a>0,b>0时,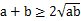 ,当且仅当a=b时等号成立)
,当且仅当a=b时等号成立)
(本小题满分10分)已知函数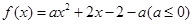 ,
,
(1)若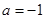 ,求函数的零点;
,求函数的零点;
(2)若函数在区间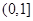 上恰有一个零点,求
上恰有一个零点,求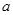 的取值范围.
的取值范围.
(本小题满分10分)已知函数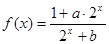 是奇函数,并且函数
是奇函数,并且函数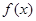 的图像经过点
的图像经过点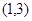 .
.
(1)求实数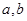 的值;
的值;
(2)求函数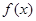 在
在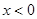 时的值域.
时的值域.
(本小题满分10分)某公司通过报纸和电视两种方式做销售某种商品的广告,根据统计资料,销售收入R(万元)与报纸广告费用x1(万元)及电视广告费用x2(万元)之间的关系有如下经验公式:R=-2x12-x22+13x1+11x2-28.
(1)若提供的广告费用共为5万元,求最优广告策略.(即收益最大的策略,其中收益=销售收入-广告费用)
(2)在广告费用不限的情况下,求最优广告策略