(本小题满分10分)已知函数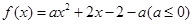 ,
,
(1)若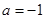 ,求函数的零点;
,求函数的零点;
(2)若函数在区间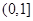 上恰有一个零点,求
上恰有一个零点,求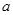 的取值范围.
的取值范围.
若函数 ,非零向量
,非零向量 ,我们称
,我们称 为函数
为函数 的“相伴向量”,
的“相伴向量”, 为向量
为向量 的“相伴函数”.
的“相伴函数”.
(1)已知函数 的最小正周期为
的最小正周期为 ,求函数
,求函数 的“相伴向量”;
的“相伴向量”;
(2)记向量 的“相伴函数”为
的“相伴函数”为 ,将
,将 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将所得的图象上所有点向左平移 个单位长度,得到函数
个单位长度,得到函数 ,若
,若 ,求
,求 的值;
的值;
(3)对于函数 ,是否存在“相伴向量”?若存在,求出
,是否存在“相伴向量”?若存在,求出 “相伴向量”;
“相伴向量”;
若不存在,请说明理由.
已知点 是抛物线
是抛物线 上不同的两点,点
上不同的两点,点 在抛物线
在抛物线 的准线
的准线 上,且焦点
上,且焦点 到直线
到直线 的距离为
的距离为 .
.
(I)求抛物线 的方程;
的方程;
(2)现给出以下三个论断:①直线 过焦点
过焦点 ;②直线
;②直线 过原点
过原点 ;③直线
;③直线 平行
平行 轴.
轴.
请你以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题,并加以证明.
如图,在四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形, ,
, ,
,
平面 平面
平面 ,若
,若
 ,
, ,
, ,
, ,且
,且 .
.
(1)求证: 平面
平面 ;
;
(2)设平面 与平面
与平面 所成二面角的大小为
所成二面角的大小为 ,求
,求 的值.
的值.
某食品厂为了检查一条自动包装流水线的生产情况,从该流水线上随机抽取40件产品作为样本,测得它们的重量(单位:克),将重量按如下区间分组: ,
, ,
, ,
, ,
, ,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
(1)在上述抽取的40件产品中任取2件,设 为合格产品的数量,求
为合格产品的数量,求 的分布列和数学期
的分布列和数学期
望 ;
;
(2)若从流水线上任取3件产品,求恰有2件合格产品的概率.
已知数列 的前
的前 项和为
项和为 满足
满足 (
(  )
)
(1)证明数列 为等比数列;
为等比数列;
(2)设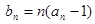 ,求数列
,求数列 的前
的前 项和
项和