已知△ABC的面积S满足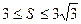 且
且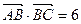 ,
,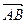 与
与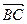 的夹角为
的夹角为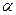
(1)求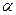 的取值范围; (2)求
的取值范围; (2)求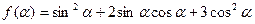 的最小值。
的最小值。
已知条件p: 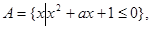 条件q:
条件q: 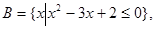 若
若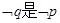 的充分但不必要条件,求实数
的充分但不必要条件,求实数 的取值范围.
的取值范围.
已知 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且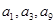 成等比数列.
成等比数列.
(1)求数列 的通项;
的通项;
(2)记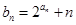 ,求数列
,求数列 的前
的前 项和
项和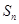
(本小题满分12分)
已知椭圆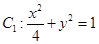 ,椭圆
,椭圆 以
以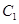 的长轴为短轴,且与
的长轴为短轴,且与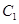 有相同的离心率.
有相同的离心率.
(1)求椭圆 的方程;
的方程;
(2)设O为坐标原点,点A,B分别在椭圆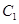 和
和 上,
上,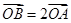 ,求直线
,求直线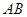 的方程.
的方程.
.(本小题满分12分)
已知函数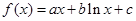 ,
,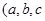 是常数)在x=e处的切线方程为
是常数)在x=e处的切线方程为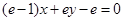 ,
, 既是函数
既是函数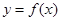 的零点,又是它的极值点.
的零点,又是它的极值点.
(1)求常数a,b,c的值;
(2)若函数 在区间(1,3)内不是单调函数,求实数m的取值范围;
在区间(1,3)内不是单调函数,求实数m的取值范围;
(3)求函数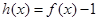 的单调递减区间,并证明:
的单调递减区间,并证明:
(本小题满分12分)
在平面直角坐标系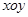 中,已知三点
中,已知三点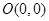 ,
,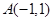 ,
, ,曲线C上任意—点
,曲线C上任意—点 满足:
满足: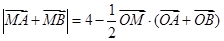 .
.
(l)求曲线C的方程;
(2)设点P是曲线C上的任意一点,过原点的直线L与曲线相交于M,N两点,若直线PM,PN的斜率都存在,并记为 ,
, .试探究
.试探究 的值是否与点P及直线L有关,并证明你的结论;
的值是否与点P及直线L有关,并证明你的结论;
(3)设曲线C与y轴交于D、E两点,点M (0,m)在线段DE上,点P在曲线C上运动.若当点P的坐标为(0,2)时, 取得最小值,求实数m的取值范围.
取得最小值,求实数m的取值范围.