(本小题满分12分)已知函数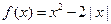 .
.
(Ⅰ)判断并证明函数的奇偶性;
(Ⅱ)利用函数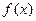 的图像指出其在
的图像指出其在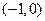 上的单调性.
上的单调性.
(满分12分)在 中,在
中,在 中,已知
中,已知 ,
, ,其面积为
,其面积为 ,
,
求 的值。
的值。
(满分12分)写出命题:“已知a,x为实数,如果关于x的不等式x2+(2a+1)x+a2+2≤0的解集非空,则a≥1”的逆命题,否命题,逆否命题并判断其真假。
如图,在四棱锥 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD, ,E是PC的中点,作
,E是PC的中点,作 交PB于点F.
交PB于点F.
(I) 证明: PA∥平面EDB;
(II) 证明:PB⊥平面EFD;
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
已知抛物线顶点在原点,焦点在x轴上,又知此抛物线上一点A(4,m)到焦点的距离为6.
(1)求此抛物线的方程;
(2)若此抛物线方程与直线 相交于不同的两点A、B,且AB中点横坐标为2,求k的值.
相交于不同的两点A、B,且AB中点横坐标为2,求k的值.