(本小题满分12分)在平面直角坐标系中,已知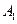
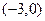 ,
,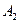
 ,
,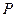 (
(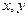 ),
),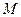
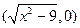 ,O为坐标原点,若实数
,O为坐标原点,若实数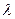 使向量
使向量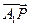 ,
,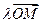 和
和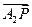 满足:
满足: ,设点P的轨迹为
,设点P的轨迹为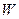 .
.
(Ⅰ)求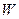 的方程,并判断
的方程,并判断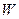 是怎样的曲线;
是怎样的曲线;
(Ⅱ)当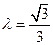 时,过点
时,过点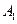 且斜率为1的直线与
且斜率为1的直线与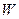 相交的另一个交点为
相交的另一个交点为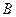 ,能否在直线
,能否在直线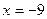 上找到一点
上找到一点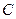 ,恰使
,恰使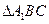 为正三角形?请说明理由.
为正三角形?请说明理由.
如图,在△ABC中,∠ABC=90°,AB=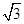 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.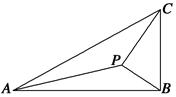
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
已知函数f(x)=2cos (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.
(1)求ω的值;
(2)设α,β∈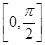 ,f
,f =-
=-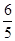 ,f
,f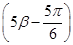 =
=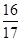 ,求cos(α+β)的值.
,求cos(α+β)的值.
受轿车在保修期内维修费等因素的影响,企业生产每辆轿车的利润与该轿车首次出现故障的时间有关.某轿车制造厂生产甲、乙两种品牌轿车,保修期均为2年.现从该厂已售出的两种品牌轿车中各随机抽取50辆,统计数据如下:
| 品牌 |
甲 |
乙 |
|||
| 首次出现故 障时间x(年) |
0<x≤1 |
1<x≤2 |
x>2 |
0<x≤2 |
x>2 |
| 轿车数量(辆) |
2 |
3 |
45 |
5 |
45 |
| 每辆利润 (万元) |
1 |
2 |
3 |
1.8 |
2.9 |
将频率视为概率,解答下列问题:
(1)从该厂生产的甲品牌轿车中随机抽取一辆,求其首次出现故障发生在保修期内的概率.
(2)若该厂生产的轿车均能售出,记生产一辆甲品牌轿车的利润为X1,生产一辆乙品牌轿车的利润为X2,分别求X1,X2的分布列.
(3)该厂预计今后这两种品牌轿车销量相当,由于资金限制,只能生产其中一种品牌的轿车.若从经济效益的角度考虑,你认为应生产哪种品牌的轿车?说明理由.
为备战2016年奥运会,甲、乙两位射击选手进行了强化训练.现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次,记录如下:
甲:8.3,9.0,7.9,7.8,9.4,8.9,8.4,8.3;
乙:9.2,9.5,8.0,7.5,8.2,8.1,9.0,8.5.
(1)画出甲、乙两位选手成绩的茎叶图;
(2)现要从中选派一人参加奥运会封闭集训,从统计学角度,你认为派哪位选手参加合理?简单说明理由;
(3)若将频率视为概率,对选手乙在今后的三次比赛成绩进行预测,记这三次成绩中不低于8.5分的次数为ξ,求ξ的分布列及均值E(ξ).
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
| 指标值分组 |
[90,94) |
[94,98) |
[98,102) |
[102,106) |
[106,110) |
| 频数 |
8 |
20 |
42 |
22 |
8 |
B配方的频数分布表
| 指标值分组 |
[90,94) |
[94,98) |
[98,102) |
[102,106) |
[106,110) |
| 频数 |
4 |
12 |
42 |
32 |
10 |
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y= 从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率)