已知函数 ,
, ,和直线m:y=kx+9,又
,和直线m:y=kx+9,又 .
.
(1)求 的值;
的值;
(2)是否存在k的值,使直线m既是曲线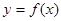 的切线,又是
的切线,又是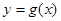 的切线;如果存在,求出k的值;如果不存在,说明理由.
的切线;如果存在,求出k的值;如果不存在,说明理由.
(3)如果对于所有 的
的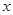 ,都有
,都有 成立,求k的取值范围.
成立,求k的取值范围.
已知命题P:方程x2+mx+1=0有两个不等的负实根;命题Q:方程4x2+4(m-2)x+1=0无实根,若“P或Q”为真,而“P且Q”为假。求实数m的取值范围。
(14分)如图,在三棱锥S—ABC中,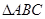 是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =
是边长为4的正三角形,平面SAC⊥平面ABC,SA =" SC" =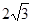 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。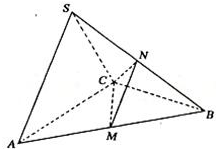
⑴ 求证:AC⊥SB;
⑵ 求二面角N—CM—B的正切值;
⑶ 求点B到平面CMN的距离。
(13分) 如图,已知椭圆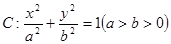 的两个焦点分别为
的两个焦点分别为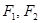 ,斜率为k的直线l过左焦点F1且与椭圆的交点为A,B与y轴交点为C,又B为线段CF1的中点,若
,斜率为k的直线l过左焦点F1且与椭圆的交点为A,B与y轴交点为C,又B为线段CF1的中点,若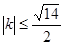 ,求椭圆离心率e的取值范围。
,求椭圆离心率e的取值范围。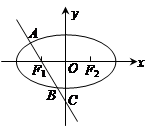
(12分)已知圆C1: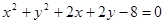 与圆C2:
与圆C2: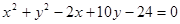 相交于A、B两点。
相交于A、B两点。
⑴ 求公共弦AB的长;
⑵ 求圆心在直线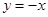 上,且过A、B两点的圆的方程;
上,且过A、B两点的圆的方程;
⑶ 求经过A、B两点且面积最小的圆的方程。
(12分) 已知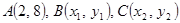 在抛物线
在抛物线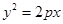 上,
上, 的重心与此抛物线的焦点F重合。
的重心与此抛物线的焦点F重合。
⑴ 写出该抛物线的标准方程和焦点F的坐标;
⑵ 求线段BC的中点M的坐标;
⑶ 求BC所在直线的方程。