(12分) 已知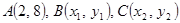 在抛物线
在抛物线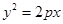 上,
上, 的重心与此抛物线的焦点F重合。
的重心与此抛物线的焦点F重合。
⑴ 写出该抛物线的标准方程和焦点F的坐标;
⑵ 求线段BC的中点M的坐标;
⑶ 求BC所在直线的方程。
如图,椭圆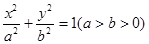 的离心率为
的离心率为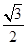 ,
,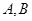 是其左右顶点,
是其左右顶点,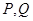 是椭圆上位于
是椭圆上位于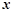 轴两侧的点(点
轴两侧的点(点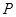 在
在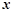 轴上方),且四边形
轴上方),且四边形 面积的最大值为4.
面积的最大值为4.
(1)求椭圆方程;
(2)设直线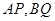 的斜率分别为
的斜率分别为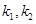 ,若
,若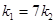 ,设△
,设△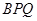 与△
与△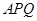 的面积分别为
的面积分别为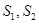 ,求
,求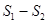 的最大值.
的最大值.
正方形 的边长为2,
的边长为2, 分别为边
分别为边 的中点,
的中点, 是线段
是线段 的中点,如图,把正方形沿
的中点,如图,把正方形沿 折起,设
折起,设 .
.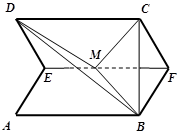
(1)求证:无论 取何值,
取何值,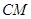 与
与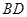 不可能垂直;
不可能垂直;
(2)设二面角 的大小为
的大小为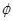 ,当
,当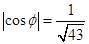 时,求
时,求 的值.
的值.
 箱中有3个黑球,6个白球,每个球被取到的概率相同,
箱中有3个黑球,6个白球,每个球被取到的概率相同,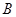 箱中没有球.我们把从
箱中没有球.我们把从 箱中取1个球放入
箱中取1个球放入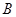 箱中,然后在
箱中,然后在 箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
箱中补上1个与取走的球完全相同的球,称为一次操作,这样进行三次操作.
(1)分别求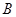 箱中恰有1个、2个、3个白球的概率;
箱中恰有1个、2个、3个白球的概率;
(2)从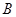 箱中一次取出2个球,记白球的个数为
箱中一次取出2个球,记白球的个数为 ,求
,求 的分布列与数学期望.
的分布列与数学期望.
△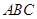 的三边为
的三边为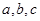 ,满足
,满足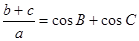 .
.
(1)求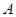 的值;
的值;
(2)求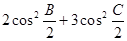 的取值范围.
的取值范围.
已知抛物线C: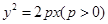 与椭圆
与椭圆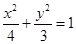 共焦点,
共焦点,
(Ⅰ)求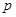 的值和抛物线C的准线方程;
的值和抛物线C的准线方程;
(Ⅱ)若P为抛物线C上位于 轴下方的一点,直线
轴下方的一点,直线 是抛物线C在点P处的切线,问是否存在平行于
是抛物线C在点P处的切线,问是否存在平行于 的直线
的直线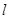 与抛物线C交于不同的两点A,B,且使
与抛物线C交于不同的两点A,B,且使 ?若存在,求出直线
?若存在,求出直线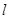 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.