如图,椭圆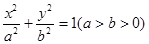 的离心率为
的离心率为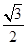 ,
,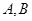 是其左右顶点,
是其左右顶点,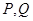 是椭圆上位于
是椭圆上位于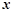 轴两侧的点(点
轴两侧的点(点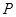 在
在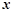 轴上方),且四边形
轴上方),且四边形 面积的最大值为4.
面积的最大值为4.
(1)求椭圆方程;
(2)设直线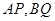 的斜率分别为
的斜率分别为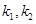 ,若
,若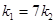 ,设△
,设△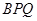 与△
与△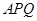 的面积分别为
的面积分别为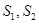 ,求
,求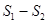 的最大值.
的最大值.
.(本小题满分10分)
在各项均为正数的数列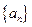 中,前
中,前 项和
项和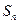 满足
满足 .
. (Ⅰ)求
(Ⅰ)求 ,并由此猜想数列
,并由此猜想数列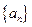 的通项公式(不需要证明);
的通项公式(不需要证明);
(Ⅱ)求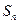 .
.
四 附加题:(本小题满分15分)
已知函数 (
( 为自然对数的底数).a
为自然对数的底数).a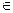 R
R
( 1)当a=1时,求函数
1)当a=1时,求函数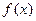 的最小值;
的最小值;
(2)若函数f(x)在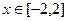 上存在极小值,求a的取值范围;
上存在极小值,求a的取值范围;
(3)若 ,证明:
,证明: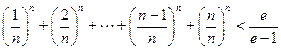 .
.
(本小题12分)
已知函数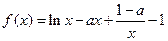
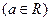 .
.
(Ⅰ)当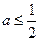 时,讨论
时,讨论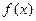 的单调性;
的单调性;
(Ⅱ)设 当
当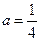 时,若对任意
时,若对任意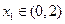 ,存在
,存在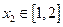 ,使
,使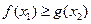 ,求实数
,求实数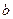 取值范围.
取值范围.
(本小题12分)
已知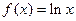 ,
, ,直线
,直线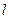 与函数
与函数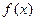 、
、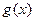 的图象都相切,且与函数
的图象都相切,且与函数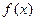 的图象的切点的横坐标为
的图象的切点的横坐标为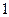 .
.
(Ⅰ)求直线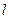 的方程及
的方程及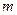 的值;
的值;
(Ⅱ)若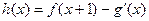 ,求函数
,求函数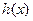 的最大值;
的最大值;
(Ⅲ)当 时,求证:
时,求证: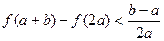 .
.
(本小题12分)
已知数列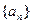 的前项和为
的前项和为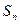 ,
,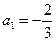 ,
,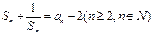
(1)求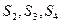
(2)猜想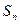 的表
的表 达式,并用数学归纳法证明。
达式,并用数学归纳法证明。