如图,已知正方形ABCD的边长为1,FD⊥平面ABCD,EB⊥平面ABCD,FD=BE=1,M为BC边上的动点.试探究点M的位置,使F—AE—M为直二面角.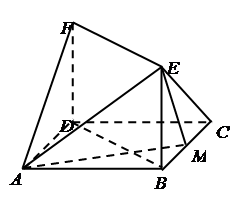
在△ABC中,角A,B,C所对的边分别为a,b,c,设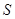 为△ABC的面积,满足
为△ABC的面积,满足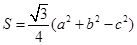 .(1)求角C的大小;(2)求
.(1)求角C的大小;(2)求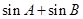 的最大值.
的最大值.
设数列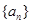 的前
的前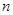 项和为
项和为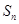 ,
,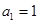 ,且
,且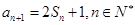 .
.
(Ⅰ)求数列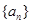 的通项公式;
的通项公式;
(Ⅱ)等差数列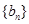 的各项均为正数,其前
的各项均为正数,其前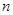 项和为
项和为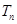 ,且
,且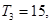 又
又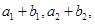
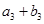 成等比数列,求
成等比数列,求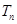 ;
;
(III)求数列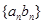 的前
的前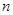 项和
项和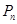 .
.
已知公差大于零的等差数列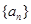 ,前
,前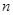 项和为
项和为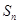 .且满足
.且满足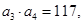
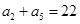 .
.
(Ⅰ)求数列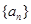 的通项公式;
的通项公式;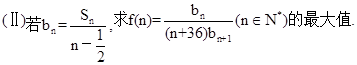
某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?
已知数列{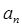 }的前n项和
}的前n项和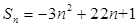 ,
,
(Ⅰ)求数列{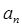 }的通项公式.
}的通项公式.
(Ⅱ)求数列{|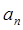 |}的前n项和
|}的前n项和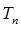 .
.