(本小题满分10分)函数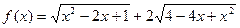 .
.
(Ⅰ)求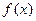 的值域;
的值域;
(Ⅱ)关于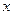 的不等式
的不等式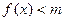 有解,求实数
有解,求实数 的范围.
的范围.
射击测试有两种方案,方案1:先在甲靶射击一次,以后都在乙靶射击;方案2:始终在乙靶射击,某射手命中甲靶的概率为 ,命中一次得3分;命中乙靶的概率为
,命中一次得3分;命中乙靶的概率为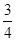 ,命中一次得2分,若没有命中则得0分,用随机变量
,命中一次得2分,若没有命中则得0分,用随机变量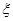 表示该射手一次测试累计得分,如果
表示该射手一次测试累计得分,如果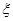 的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
(1)如果该射手选择方案1,求其测试结束后所得分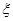 的分布列和数学期望E
的分布列和数学期望E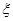 ;
;
(2)该射手选择哪种方案通过测试的可能性大?请说明理由。
解不等式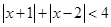
选修4-4:坐标系与参数方程[ (本小题满分10分)
己知直线  的参数方程为
的参数方程为 (t为参数),圆C的参数方程为
(t为参数),圆C的参数方程为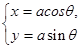 .(a>0.
.(a>0. 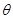 为参数),点P是圆C上的任意一点,若点P到直线
为参数),点P是圆C上的任意一点,若点P到直线 的距离的最大值为
的距离的最大值为 ,求a的值。
,求a的值。
(选修4-2:矩阵与变换)
已知矩阵 ,试求曲线
,试求曲线 在矩阵
在矩阵 变换下的函数解析式.
变换下的函数解析式.
(本小题满分10分,几何证明选讲)
如图,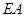 与圆
与圆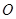 相切于点
相切于点 ,
, 是
是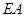 的中点,过点
的中点,过点 引圆
引圆 的割线,与圆
的割线,与圆 相交于点
相交于点 ,连结
,连结 .
.
求证: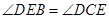 .
.