(本小题满分12分)在一个圆锥体的培养房内培养了40只蜜蜂,准备进行某种实验,过圆锥高的中点有一个不计厚度且平行于圆锥底面的平面把培养房分成两个实验区,其中小锥体叫第一实验区,圆台体叫第二实验区,且两个实验区是互通的。假设蜜蜂落入培养房内任何位置是等可能的,且蜜蜂落入哪个位置相互之间是不受影响的。
(1)求蜜蜂落入第二实验区的概率;
(2)若其中有10只蜜蜂被染上了红色,求恰有一只红色蜜蜂落入第二实验区的概率.
(本小题满分13分)如图,在正三棱柱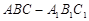 中,已知
中,已知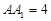 ,
,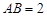 ,
,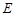 是
是 的中点,
的中点,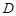 在棱
在棱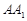 上.
上.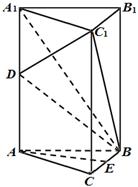
(1)求异面直线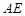 与
与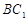 所成角;
所成角;
(2)若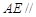 平面
平面 ,求
,求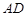 长;
长;
(3)在棱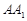 上是否存在点
上是否存在点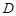 ,使得二面角
,使得二面角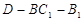 的大小等于
的大小等于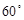 ,若存在,求
,若存在,求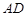 的长;若不存在,说明理由.
的长;若不存在,说明理由.
(本小题满分13分)椭圆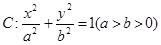 的左、右焦点分别是
的左、右焦点分别是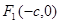 ,
,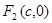 ,过
,过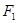 斜率为1的直线与椭圆
斜率为1的直线与椭圆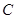 相交于
相交于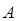 ,
,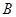 两点,且
两点,且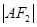 ,
,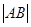 ,
,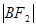 成等差数列.
成等差数列.
(1)请探求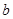 与
与 的关系;
的关系;
(2)设点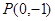 在线段
在线段 的垂直平分线上,求椭圆
的垂直平分线上,求椭圆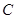 的方程.
的方程.
(本小题满分12分)如图所示,直三棱柱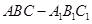 中,
中,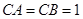 ,
, ,棱
,棱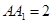 ,
, 分别是
分别是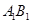 、
、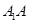 的中点.
的中点.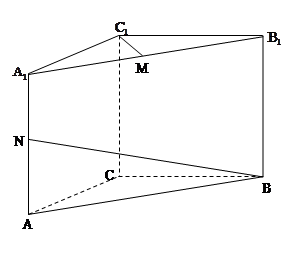
(1)求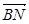 的长;
的长;
(2)求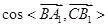 的值;
的值;
(3)求证: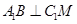 .
.
(本小题满分12分) 已知命题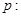
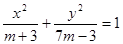 表示焦点在
表示焦点在 轴的双曲线,命题
轴的双曲线,命题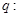
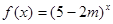 是增函数,若
是增函数,若 或
或 为真命题,
为真命题, 且
且 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
(本小题满分12分) 已知曲线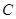 :
:  ,求曲线
,求曲线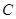 在
在 轴上的所截的线段的长度为1的充要条件,证明你的结论.
轴上的所截的线段的长度为1的充要条件,证明你的结论.