(本小题满分14分)
已知数列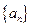 满足
满足
(I)证明:数列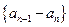 是等比数列;
是等比数列;
(II)求数列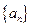 的通项公式;
的通项公式;
(III)若数列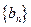 满足
满足 证明
证明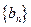 是等差数列
是等差数列
(本小题满分12分)
已知 :函数
:函数 的定义域为
的定义域为 ;
; 如果命题“
如果命题“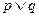 为真,
为真, 为假”,求实数
为假”,求实数 的取值范围.
的取值范围.
(本小题满分14分)
设函数
(Ⅰ)当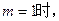 曲线
曲线 处的切线斜率
处的切线斜率
(Ⅱ)求函数的单调区间与极值;
(Ⅲ)已知函数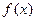 有三个互不相同的零点0,
有三个互不相同的零点0, ,且
,且 .若对任意的
.若对任意的 ,
,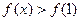 恒成立,求m的取值范围.
恒成立,求m的取值范围.
(本小题满分14分)
已知函数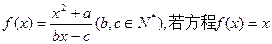 有且只有两个相异实根0,2,且
有且只有两个相异实根0,2,且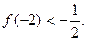
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)已知各项均不为1的数列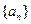 满足
满足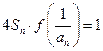 ,求通
,求通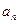 ,
,
(Ⅲ)设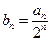 ,求数列
,求数列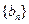 的前
的前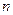 项和
项和 .
.
如图6,在平面直角坐标系 中,设点
中,设点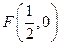 ,直线
,直线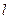 :
: ,点
,点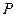 在直线
在直线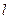 上移动,
上移动,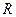 是线段
是线段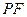 与
与 轴的交点,
轴的交点, 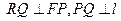 .
.
(I)求动点 的轨迹的方程
的轨迹的方程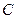 ;
;
(II)设圆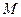 过
过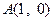 ,且圆心
,且圆心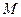 在曲线
在曲线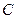 上,
上, 是圆
是圆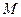 在
在 轴上截得的弦,当
轴上截得的弦,当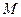 运动时弦长
运动时弦长 是否为定值?请说明理由.
是否为定值?请说明理由.
(本小题满分14分)
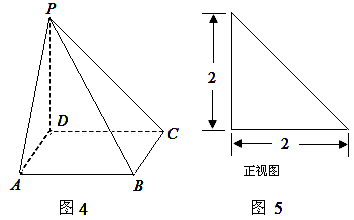
如图4,四棱锥P-ABCD的底面ABCD是正方形,PD垂直于底面ABCD,已知四棱锥的正视图,如图5所示,
(Ⅰ)若M是PC的中点,证明:DM⊥平面PBC;
(Ⅱ)求棱锥A-BDM的体积.