我校社团联即将举行一届象棋比赛，规则如下：两名选手比赛时，每局胜者得
分，负者得
分，比赛进行到有一人比对方多
分或打满
局时结束.假设选手甲与选手乙比赛时，甲每局获胜的概率皆为
，且各局比赛胜负互不影响.
（Ⅰ）求比赛进行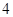
局结束，且乙比甲多得分的概率；
（Ⅱ）设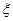
表示比赛停止时已比赛的局数，求随机变量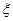的分布列和数学期望．
某工厂生产一种仪器的元件，由于受生产能力和技术水平的限制，会产生一些次品，根据经验知道，其次品率
与日产量
（万件）之间大体满足关系：
（其中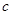
为小于6的正常数）（注：次品率=次品数/生产量，如
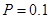表示每生产10件产品，有1件为次品，其余为合格品），已知每生产1万件合格的仪器可以盈利2万元，但
每生产1万件次品将亏损1万元，故
厂方希望定出合适的日产量．（1）试将生产这种仪器的元件每天的盈利额
（万元）表示为日产量（万件）的函数；（2）当日产量为多少时，可获得最大利润？
已知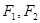
是椭圆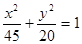
的两个焦点，
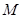是椭圆上的第一象限内的点，且
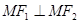．（1）求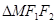
的周长；（2）求点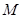的坐标．
设p ：指数函数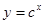
在R上是减函数；q：
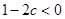。若p∨q是真命题，p∧q是假命题，求
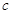的取值范围。
已知中心在原点的双曲线C的右焦点为（2,0），右顶点为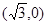
。
（1）求双曲线C的方程；
（2）若直线l：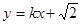
与双曲线C恒有两个不同的交点A和B，且
（其中O为原点），求k的取值范围.
若函数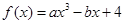
，当x=2时，函数f（x）有极值
．
（1）求函数f（x）的解析式；（2）若函数f（x）=k有3个解，求实数k的取值范围.