已知数列 的首项为
的首项为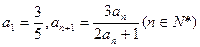 (1)若
(1)若 ,求证:数列
,求证:数列 是等比数列;(2)若
是等比数列;(2)若 ,求数列
,求数列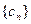 的前
的前 项和.
项和.
已知函数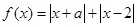
(1)当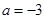 时,求不等式
时,求不等式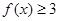 的解集;(2)若
的解集;(2)若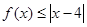 的解集包含
的解集包含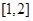 ,求
,求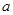 的取值范围.
的取值范围.
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sinθ,ρcos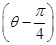 =2
=2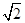 .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点.已知直线PQ的参数方程为 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值.
如图所示,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
(1)证明:DB=DC;
(2)设圆的半径为1,BC= ,延长CE交AB于点F,
,延长CE交AB于点F,
求△BCF外接圆的半径.
已知函数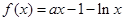
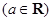 .
.
(1)讨论函数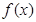 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数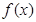 在
在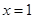 处取得极值,对
处取得极值,对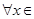
 ,
,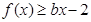 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)当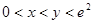 且
且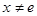 时,试比较
时,试比较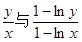 的大小
的大小
(本小题满分12分)
已知椭圆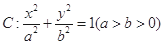 的离心率为
的离心率为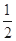 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线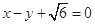 相切,过点
相切,过点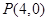 且不垂直于
且不垂直于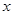 轴的直线
轴的直线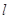 与椭圆
与椭圆 相交于
相交于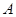 、
、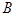 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)求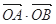 的取值范围;
的取值范围;
(3)若 点关于
点关于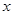 轴的对称点是
轴的对称点是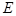 ,证明:直线
,证明:直线 与
与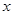 轴相交于定点.
轴相交于定点.