已知函数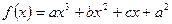 (
(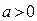 )的单调递减区间是
)的单调递减区间是 ,且满足
,且满足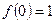 .
.
(Ⅰ)求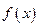 的解析式;
的解析式;
(Ⅱ)对任意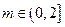 , 关于
, 关于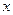 的不等式
的不等式 在
在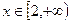 上有解,求实数
上有解,求实数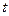 的取值范围.
的取值范围.
设命题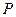 :
: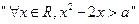 ,命题
,命题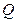 :
: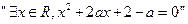 ;
;
如果“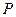 或
或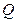 ”为真,“
”为真,“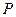 且
且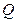 ”为假,求
”为假,求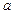 的取值范围。(在数学中“所有”一词,叫全称量词,用符号“
的取值范围。(在数学中“所有”一词,叫全称量词,用符号“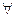 ”表示;“存在”一词,叫做存在量词,用符号“
”表示;“存在”一词,叫做存在量词,用符号“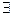 ”表示
”表示 )
)
(本小题满分14分)已知函数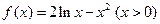 。
。
(1)求函数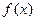 的单调区间与最值;
的单调区间与最值;
(2)若方程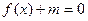 在区间
在区间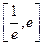 内有两个不相等的实根,求实数
内有两个不相等的实根,求实数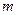 的取值范围;(其中e为自然对数的底数)
的取值范围;(其中e为自然对数的底数)
(3)如果函数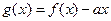 的图像与x轴交于两点
的图像与x轴交于两点 ,且
,且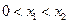 ,求证:
,求证: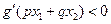 (其中,
(其中,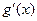 是
是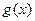 的导函数,正常数
的导函数,正常数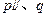 满足
满足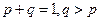 )
)
(本小题满分14分)
某市环保研究所对市中心每天环境污染情况进行调查研究后,发现一天中环境综合污染指数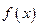 与时间x(小时)的关系为
与时间x(小时)的关系为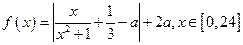 ,其中
,其中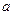 是与气象有关的参数,且
是与气象有关的参数,且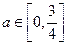 ,若用每天
,若用每天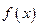 的最大值为当天的综合污染指数,并记作
的最大值为当天的综合污染指数,并记作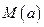 .
.
(1)令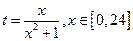 ,求t的取值范围;
,求t的取值范围;
(2)求函数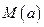 ;
;
(3)市政府规定,每天的综合污染指数不得超过2,试问目前市中心的综合污染是否超标?请说明理由。
(本小题满分14分)
已知函数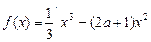
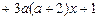 ,a∈R.
,a∈R.
(1)当a=0时,求曲线y=f(x)在点(3,f(3))处的切线方程:
(2)当函数y=f'(x)在(0,4)上有唯一的零点时,求实数a的取值范围.
(本小题满分14分)已知△ABC三个内角A、B、C的对边为a、b、c,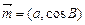 ,
, ,a≠b,已知
,a≠b,已知 .
.
(1)判断三角形的形状,并说明理由。
(2)若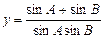 ,试确定实数y的取值范围.
,试确定实数y的取值范围.