(本小题满分14分)已知函数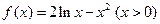 。
。
(1)求函数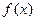 的单调区间与最值;
的单调区间与最值;
(2)若方程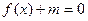 在区间
在区间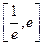 内有两个不相等的实根,求实数
内有两个不相等的实根,求实数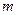 的取值范围; (其中e为自然对数的底数)
的取值范围; (其中e为自然对数的底数)
(3)如果函数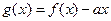 的图像与x轴交于两点
的图像与x轴交于两点 ,且
,且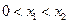 ,求证:
,求证: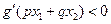 (其中,
(其中,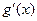 是
是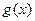 的导函数,正常数
的导函数,正常数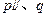 满足
满足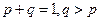 )
)
选修4-5:不等式选讲
设函数 ,
,
(Ⅰ)证明
(Ⅱ)若不等式 的解2集非空,求
的解2集非空,求 的取值范围。
的取值范围。
选修4-4:坐标系与参数方程
在平面直角坐标系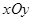 中,
中,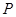 是直线
是直线 上的一点,
上的一点,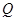 是射线
是射线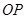 上的一点,满足
上的一点,满足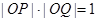 。
。
(Ⅰ)求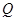 点的轨迹;
点的轨迹;
(Ⅱ)设点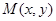 是(Ⅰ)中轨迹上任意一点,求
是(Ⅰ)中轨迹上任意一点,求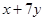 的最大值。
的最大值。
选修4-1:几何证明选讲
过以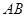 为直径的圆上
为直径的圆上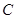 点作直线交圆于
点作直线交圆于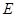 点,交
点,交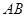 挺长线于
挺长线于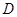 点,过
点,过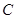 点作圆的切线交
点作圆的切线交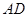 于
于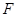 点,交
点,交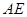 挺长线于
挺长线于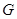 点,且
点,且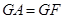 。
。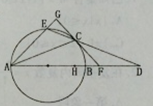
(Ⅰ)求证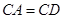 ;
;
(Ⅱ)设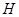 为
为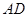 的中点,求证
的中点,求证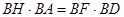
已知函数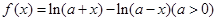 曲线
曲线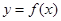 在点
在点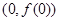 处的切线方程为
处的切线方程为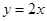
(1),求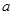 的值;
的值;
(2)求证:当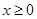 时,
时,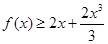 。
。
已知椭圆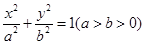 的,离心率为
的,离心率为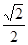 ,
,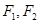 是其焦点,点
是其焦点,点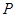 在椭圆上。
在椭圆上。
(Ⅰ)若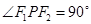 ,且
,且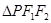 的面积等于
的面积等于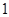 。求椭圆的方程;
。求椭圆的方程;
(Ⅱ)直线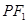 交椭圆于另一点
交椭圆于另一点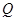 ,分别过点
,分别过点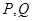 作直线
作直线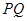 的垂线,交
的垂线,交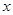 轴于点
轴于点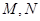 ,当
,当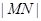 取最小值时,求直线
取最小值时,求直线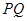 的斜率。
的斜率。