已知椭圆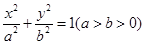 的,离心率为
的,离心率为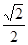 ,
,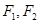 是其焦点,点
是其焦点,点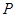 在椭圆上。
在椭圆上。
(Ⅰ)若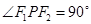 ,且
,且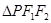 的面积等于
的面积等于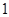 。求椭圆的方程;
。求椭圆的方程;
(Ⅱ)直线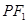 交椭圆于另一点
交椭圆于另一点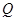 ,分别过点
,分别过点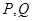 作直线
作直线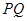 的垂线,交
的垂线,交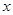 轴于点
轴于点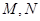 ,当
,当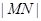 取最小值时,求直线
取最小值时,求直线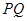 的斜率。
的斜率。
(本小题满分14分)已知向量
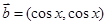 ,函数
,函数

(Ⅰ)求函数 在
在 上的值域;
上的值域;
(Ⅱ)当 时,若
时,若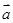 与
与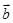 共线,求
共线,求 的值.
的值.
(本小题满分14分)已知直线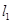 的方程为
的方程为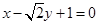 ,其倾斜角为
,其倾斜角为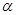 .过点
.过点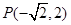 的直线
的直线 的倾斜角为
的倾斜角为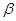 ,且
,且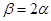 .
.
(Ⅰ)求直线 的一般式方程; (Ⅱ)求
的一般式方程; (Ⅱ)求 的值.
的值.
如图,已知椭圆 的焦点和上顶点分别为
的焦点和上顶点分别为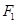 、
、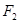 、
、 ,我们称
,我们称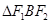 为椭圆
为椭圆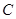 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
(1)已知椭圆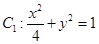 和
和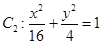 ,判断
,判断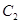 与
与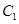 是否相似,如果相似则求出
是否相似,如果相似则求出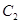 与
与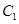 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)若与椭圆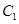 相似且半短轴长为
相似且半短轴长为 的椭圆为
的椭圆为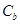 ,且直线
,且直线 与椭圆为
与椭圆为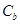 相交于两点
相交于两点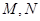 (异于端点),试问:当
(异于端点),试问:当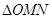 面积最大时,
面积最大时,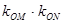 是否与
是否与 有关?并证明你的结论.
有关?并证明你的结论.
(3)根据与椭圆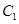 相似且半短轴长为
相似且半短轴长为 的椭圆
的椭圆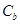 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
已知函数
(1)若对任意的 恒成立,求实数
恒成立,求实数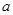 的最小值.
的最小值.
(2)若 且关于
且关于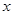 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)设各项为正的数列 满足:
满足: 求证:
求证: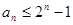
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直, AA1=AB=AC=1,AB⊥AC, M是CC1的中点, N是BC的中点,点P在线段A1B1上,且满足A1P=lA1B1.
(1)证明:PN⊥AM.
(2)当λ取何值时,直线PN与平面ABC所成的角θ最大?并求该角最大值的正切值.
(3)是否存在点P,使得平面 PMN与平面ABC所成的二面角为45°.若存在求出l的值,若不存在,说明理由.