选修4-1:几何证明选讲
过以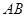 为直径的圆上
为直径的圆上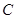 点作直线交圆于
点作直线交圆于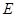 点,交
点,交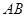 挺长线于
挺长线于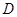 点,过
点,过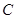 点作圆的切线交
点作圆的切线交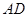 于
于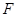 点,交
点,交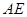 挺长线于
挺长线于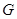 点,且
点,且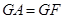 。
。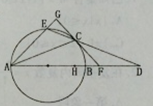
(Ⅰ)求证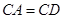 ;
;
(Ⅱ)设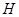 为
为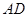 的中点,求证
的中点,求证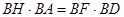
(本小题满分14分)下面是利用UNTIL循环设计的计算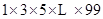 的一个算法程序.
的一个算法程序.
S=1
i=1
DO
①
i=i+2
LOOP UNTIL ②
PRINT S
END
(Ⅰ)请将其补充完整,并转化为WHILE循环;
(Ⅱ)绘制出该算法的流程图.
(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量( 吨)与相应的生产能耗
吨)与相应的生产能耗 (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
 |
3 |
4 |
5 |
6 |
 |
2.5 |
3 |
4 |
4.5 |

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出 关于
关于 的线性回归方程
的线性回归方程 ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式  ,
, )
)
(本小题满分12分)在育民中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.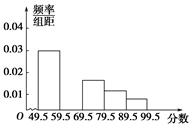
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数是多少?
(3)求两个班参赛学生的成绩的中位数。
(本小题满分12分)已知 ,
,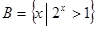 ,
,
(1)求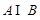 和
和 ;
;
(2)若记符号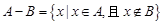 ,
,
①在图中把表示“集合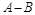 ”的部分用阴影涂黑;
”的部分用阴影涂黑;
②求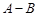 和
和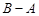 .
.
(本小题满分15分)设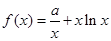 ,
,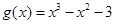 .
.
(1)当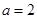 时,求曲线
时,求曲线 在
在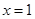 处的切线的斜率;
处的切线的斜率;
(2)如果存在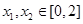 ,使得
,使得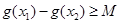 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数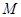 ;
;
(3)如果对于任意 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.