设二次函数f(x)=ax2+bx+c(a>0),方程f(x)﹣x=0的两个根x1,x2满足:0<x1<x2<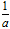 .
.
(1)当x∈(0, x1)时,证明x<f(x)<x1;
(2)设函数f(x)的图象关于直线x=x0对称,证明x0<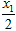 .
.
在△ABC中 ,角 、
、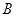 、
、 所对的边分别为
所对的边分别为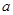 、
、 、
、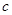 ,已知向量
,已知向量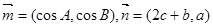 ,且
,且 .
.
(Ⅰ) 求角A的大小;
(Ⅱ) 若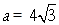 ,
, ,求△ABC的面积.
,求△ABC的面积.
某普通高中共有教师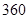 人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
人,分为三个批次参加研修培训,在三个批次中男、女教师人数如下表所示:
| 第一批次 |
第二批次 |
第三批次 |
|
| 女教师 |
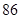 |
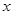 |
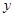 |
| 男教师 |
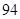 |
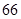 |
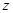 |
已知在全体教师中随机抽取1名,抽到第二、三批次中女教师的概率分别是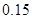 、
、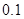 .
.
(Ⅰ)求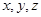 的值;
的值;
(Ⅱ)为了调查研修效果,现从三个批次中按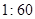 的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
的比例抽取教师进行问卷调查,三个批次被选取的人数分别是多少?
(Ⅲ)若从(Ⅱ)中选取的教师中随机选出两名教师进行访谈,求参加访谈的两名教师“分别来自两个批次”的概率.
已知函数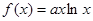 图像上点
图像上点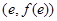 处的切线与直线
处的切线与直线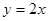 平行(其中
平行(其中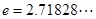 ),
),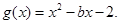
(I)求函数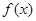 的解析式;
的解析式;
(II)求函数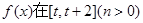 上的最小值;
上的最小值;
(III)对一切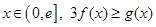 恒成立,求实数
恒成立,求实数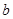 的取值范围。
的取值范围。
已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线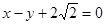 的距离为3.
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线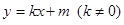 相交于不同的两点M、N.当
相交于不同的两点M、N.当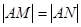 时,求m的取值范围.
时,求m的取值范围.
已知函数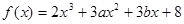 在
在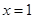 及
及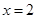 处取得极值.
处取得极值.
(1)求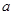 、
、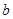 的值;(2)求
的值;(2)求 的单调区间.
的单调区间.