已知函数f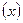 =" x" +
=" x" + ,
,
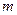 为常数,且
为常数,且 是奇函数且在区间
是奇函数且在区间 上是减函数.
上是减函数.
(1)求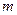 的值; (2)判断
的值; (2)判断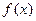 的奇偶性;
的奇偶性;
(3)函数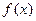 在
在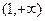 上是增函数还是减函数?并证明之.
上是增函数还是减函数?并证明之.
(本小题满分13分)某初级中学共有学生2000名,各年级男、女生人数如下表. 
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19 .
(1)求x的值;
(2)现用分层抽样的方法在全校抽取48名学生, 问应在初三年级抽取多少名?
(3)已知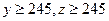 ,求初三年级中女生比男生多的概率。
,求初三年级中女生比男生多的概率。
(本大题共15分)已知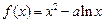 在
在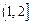 上是增函数,
上是增函数, 在
在 上是减函数.(1)求
上是减函数.(1)求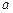 的值;(2)设函数
的值;(2)设函数 在
在 上是增函数,且对于
上是增函数,且对于 内的任意两个变量
内的任意两个变量 ,恒有
,恒有 成立,求实数
成立,求实数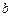 的取值范围;(3)设
的取值范围;(3)设 ,求证:
,求证: .
.
(本大题共15分) 如图,F是椭圆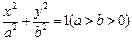 的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为
的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为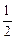 ,点C在x轴上,
,点C在x轴上,
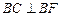 ,B、C、F三点确定的圆M恰好与
,B、C、F三点确定的圆M恰好与
直线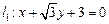 相切.(1)求椭圆的方程;
相切.(1)求椭圆的方程;
(2)过点A的直线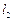 与圆M交于P、Q两点,
与圆M交于P、Q两点,
且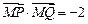 ,求直线
,求直线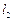 的方程.
的方程.
(本大题共14分)一袋中装有分别标记着1,2,3,4数字的4只小球,每次从袋中取出一只球,设每只小球被取到的可能性相同.(1)若每次取出的球不放回袋中,求恰好第三次取到标号为3的球的概率;(2)若每次取出的球放回袋中,然后再取出一只球,现连续取三次球,若三次取出的球中标号最大的数字为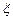 ,求
,求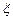 的概率分布列与期望.
的概率分布列与期望.
(本大题共14分)已知数列 的前n项和
的前n项和 ,且
,且 是
是 与1的等差中项.
与1的等差中项.
(1)求数列 和数列
和数列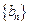 的通项公式;(2)若
的通项公式;(2)若 ,求
,求 ;
;
(3)若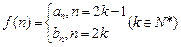 ,是否存在
,是否存在 使得
使得 ,并说明理由.
,并说明理由.