某学校举行知识竞赛,第一轮选拔共设有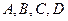 四个问题,规则如下:
四个问题,规则如下:
① 每位参加者计分器的初始分均为10分,答对问题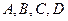 分别加1分、2分、3分、6分,答错任一题减2分;
分别加1分、2分、3分、6分,答错任一题减2分;
② 每回答一题,计分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局,当累计分数大于或等于14分时,答题结束 ,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③ 每位参加者按问题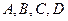 顺序作答,直至答题结束.
顺序作答,直至答题结束.
假设甲同学对问题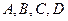 回答正确的概率依次为
回答正确的概率依次为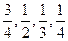 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用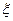 表示甲同学本轮答题结束时答题的个数,求
表示甲同学本轮答题结束时答题的个数,求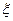 的分布列和数学的
的分布列和数学的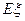 .
.
已知在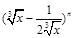 的展开式中,第6项
的展开式中,第6项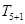 为常数项.
为常数项.
(1)求n;
(2)求展开式中所有的有理项.
某射手击中目标的概率为0.8,每次射击的结果相互独立,现射击10次,问他最有可能射中几次?
已知函数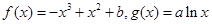 .
.
(1)若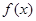 在
在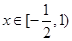 上的最大值为
上的最大值为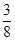 ,求实数
,求实数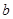 的值;
的值;
(2)若对任意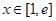 ,都有
,都有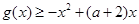 恒成立,求实数
恒成立,求实数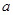 的取值范围;
的取值范围;
(3)在(1)的条件下,设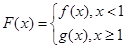 ,对任意给定的正实数
,对任意给定的正实数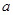 ,曲线
,曲线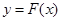 上是否存在两点
上是否存在两点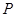 、
、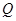 ,使得
,使得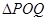 是以
是以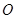 (
(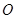 为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在
为坐标原点)为直角顶点的直角三角形,且此三角形斜边中点在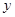 轴上?请说明理由。
轴上?请说明理由。
已知中心在坐标原点焦点在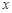 轴上的椭圆C,其长轴长等于4,离心率为
轴上的椭圆C,其长轴长等于4,离心率为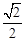 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点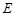 (0,1), 问是否存在直线
(0,1), 问是否存在直线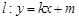 与椭圆
与椭圆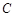 交于
交于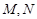 两点,且
两点,且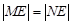 ?若存在,求出
?若存在,求出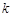 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
已知函数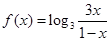 .
.
(1)证明函数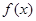 的图像关于点
的图像关于点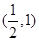 对称;
对称;
(2)若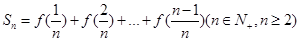 ,求
,求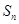 ;
;
(3)在(2)的条件下,若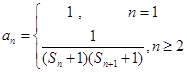
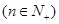 ,
,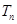 为数列
为数列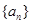 的前
的前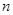 项和,若
项和,若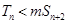 对一切
对一切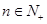 都成立,试求实数
都成立,试求实数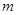 的取值范围.
的取值范围.