(本题满分13分)
已知函数 在
在 上是减函数,在
上是减函数,在 上是增函数,函数
上是增函数,函数 在
在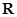 上有三个零点.
上有三个零点.
(1)求 的值;
的值;
(2)若1是其中一个零点,求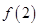 的取值范围;
的取值范围;
(3)若 ,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
,试问过点(2,5)可作多少条直线与曲线y=g(x)相切?请说明理由。
(本题满分13分)
对于给定数列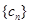 ,如果存在实常数
,如果存在实常数 使得
使得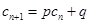 对于任意
对于任意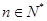 都成立,我们称数列
都成立,我们称数列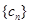 是 “M类数列”.
是 “M类数列”.
(1)若 ,
,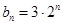 ,
,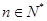 ,数列
,数列 、
、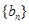 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数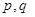 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列 是“M类数列”,则数列
是“M类数列”,则数列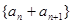 也是“M类数列”;
也是“M类数列”;
(3)若数列 满足
满足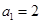 ,
,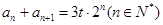 ,
,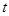 为常数.求数列
为常数.求数列 前
前 项的和.
项的和.
(本小题满分13分)
运货车以每小时x千米的速度匀速行驶130千米(60≤x≤100),假设汽油的价格是每升2元,而汽车每小时耗油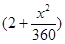 升,付给司机的工资是每小时14元。
升,付给司机的工资是每小时14元。
(1)求这次行车总费用y关于x的表达式
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值。
(本小题满分13分)已知等差数列 的前
的前 项和为
项和为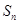 ,且
,且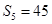 ,
,
(1)求数列 的通项公式
的通项公式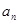 ;
;
(2)若数列 满足
满足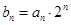 ,求数列
,求数列 的前
的前 项和
项和
在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足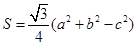 。
。
(Ⅰ)求角C的大小;
(Ⅱ)求 的最大值。
的最大值。