.(本小题满分12分)
已知二次函数 对
对 都满足
都满足 且
且 ,设函数
,设函数 (
(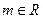 ,
, ).
).
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)若 ,使
,使 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅲ)设 ,
, ,求证:对于
,求证:对于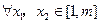 ,恒有
,恒有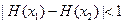 .
.
(本小题满分12分)
某公园的大型中心花园的边界为椭圆,花园内种植各种花草. 为增强观赏性,在椭圆内以其
中心为直角顶点且关于中心对称的两个直角三角形内种植名贵花草(如图),并以该直角三角
形斜边开辟观赏小道(其中的一条为线段 ). 某园林公司承接了该中心花园的施工建设,
). 某园林公司承接了该中心花园的施工建设,
在施工时发现,椭圆边界上任意一点到椭圆两焦点的距离和为4(单位:百米),且椭圆上点
到焦点的最近距离为1(单位:百米).
(Ⅰ)以椭圆中心为原点建立如图的坐标系,求该椭圆的标准方程;
(Ⅱ)请计算观赏小道的长度(不计小道宽度)的最大值.
 |
(本小题满分12分)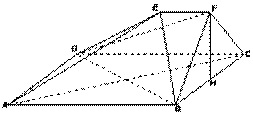
如图,在多面体ABCDEF中,ABCD是正方形,AB=2EF=2, ,EF⊥FB,∠BFC=
,EF⊥FB,∠BFC= ,BF=FC,H为BC的中点.
,BF=FC,H为BC的中点.
(Ⅰ)求证: 平面EDB;
平面EDB;
(Ⅱ)求证:AC⊥平面EDB;
(Ⅲ)求四面体B—DEF的体积.
(本小题满分12分)
某中学研究性学习小组,为了考察高中学生的作文水平与爱看课外书的关系,在本校高三年级随机调查了 50名学生.调査结果表明:在爱看课外书的25人中有18人作文水平好,另7人作文水平一般;在不爱看课外书的25人中有6人作文水平好,另19人作文水平一般.
(Ⅰ)试根据以上数据完成以下2×2列联表,并运用独 立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
立性检验思想,指出有多大把握认为中学生的作文水平与爱看课外书有关系?
高中学生的作文水平与爱看课外书的2×2列联表
| 爱看课外书 |
不爱看课外书 |
总计 |
|
作文水平 好 好 |
|||
| 作文水平一般 |
|||
| 总计 |
(Ⅱ)将其中某5名爱看课外书且作文水平好的学生分别编号为1、2、3、4、5,某5名爱看课外书且作文水平一般的学生也 分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
分别编号为1、2、3、4、5,从这两组学生中各任选1人进行学习交流,求被选取的两名学生的编号之和为3的倍数或4的倍数的概率.
参考公式: ,其中
,其中 .
.
参考数据:
 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(本小题满分12分)
锐角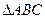 中,角A、B、
中,角A、B、 C所对的边分别为
C所对的边分别为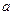 、
、 、
、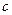 ,且
,且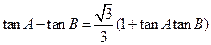 .
.
(Ⅰ)若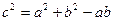 ,求角A、B、C大小;
,求角A、B、C大小;
(Ⅱ)已知向量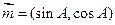 ,
,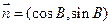 ,求
,求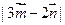 的取值范围.
的取值范围.