弹簧振子以O点为平衡位置在B、C两点之间做简谐运动.B、C相距20 cm.某时刻振子处于B点.经过0.5 s，振子首次到达C点.求：
（1）振动的周期和频率；
（2）振子在5 s内通过的路程及位移大小；
（3）振子在B点的加速度大小跟它距O点4 cm处P点的加速度大小的比值.
已知一汽车在平直公路上运动，它的位移-时间图像如甲图所示，
（1）根据图像在图乙所示的位置坐标轴上标出O、A、B、C、D、E各点代表的汽车的位置；
（2）求出前4s内的平均速度；
（3）求出第5s末的瞬时速度；
（4）求出第7s末的加速度。
如图所示，水平放置的平行板电容器，原来AB两板不带电，B板接地，它的极板长
，两板间距离
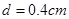，现有一微粒质量
，带电荷量
，以一定初速度从两板中间平行于极板射入，由于重力作用微粒恰好能落到A板的中点O处，取
，试求：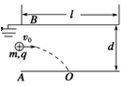
（1）带电粒子入射速度
的大小
（2）现使电容器带上电荷，使带电微粒能从平行板电容器的右侧射出，则带电后A板的电势为多少
如下图所示，在水平向右的匀强电场中，有一光滑绝缘导轨，导轨由水平部分和它连接的位于竖直平面的半圆环ABC构成，现距环最低点A为L的O处有一质量为m的带正电的小球，小球从静止开始沿水平轨道进入圆环，若小球所受电场力与其重力大小相等，圆环轨道的半径为R，则L必须满足什么条件才能使得小球在圆环上运动时不脱离圆环？
一根长为l的丝线吊着一质量为m，带电荷量为q的小球静止在水平向右的匀强电场中，如图所示，丝线与竖直方向成37°角，现突然将该电场方向变为向下且大小不变，不考虑因电场的改变而带来的其他影响(重力加速度为g)，求：
(1)匀强电场的电场强度的大小；(sin37°＝0.6，cos37°＝0.8)，
(2)小球经过最低点对丝线的拉力．
把一个电量为q＝5×10－9 C的正电荷从距电场无穷远处移到电场中M点，电荷克服电场力做功WM＝6.0×10－3 J，如果把该点电荷从距电场无穷远处移到电场中N点，电荷克服电场力做功WN＝3.6×10－3 J，已知点电荷质量是3.0×10－9 kg，取无穷远处为零电势点，求：
(1)M、N点的电势是多少？
(2)M、N点的电势差是多少？把该点电荷从M点移到N点电场力做功是多少？
(3)如把点电荷从M点由静止释放，它能获得的最大速度是多少？