(本小题满分13分)在某校组织的一次篮球定点投篮训练中,规定每人最多投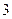 次;在
次;在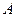 处每投进一球得
处每投进一球得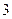 分,在
分,在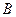 处每投进一球得
处每投进一球得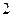 分;如果前两次得分之和超过
分;如果前两次得分之和超过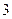 分即停止投篮,否则投第三次,某同学在
分即停止投篮,否则投第三次,某同学在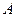 处的命中率
处的命中率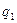 为
为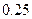 ,在
,在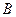 处的命中率为
处的命中率为 ,该同学选择先在
,该同学选择先在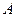 处投一球,以后都在
处投一球,以后都在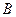 处投,用
处投,用 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
 |
0 |
2 |
3 |
4 |
5 |
| p |
0.03 |
P1 |
P2 |
P3  |
P4 |
(1)求 的值;
的值;
(2)求随机变量 的数学期望E
的数学期望E .
.
(本小题满分12分)
为了绿化城市,准备在如图所示的区域内修建一个矩形PQRC的草坪,且PQ∥BC,RQ⊥BC,另外△AEF的内部有一文物保护区不能占用,经测量AB =100m,BC=80m,AE=30m,AF=20m.
=100m,BC=80m,AE=30m,AF=20m.
(1)求直线EF的方程;
(2)应如何设计才能使草坪的占地面积最大?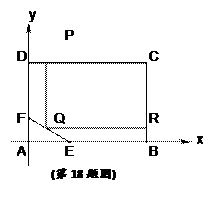

(本小题满分14分)
从某学校高一年级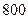 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和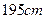 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组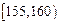 .第二组
.第二组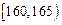 ;…第八组
;…第八组 ,右图
,右图
是按上述分组方法得到的条形图.

(1)根据已知条件填写下面表格:
| 组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 样本数 |
 |
(2)估计这所学校高一年级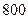 名学生中身高在
名学生中身高在 以上(含
以上(含 )的人数;
)的人数;
(3)在样本中,若第二组有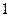 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有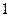 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
(本小题满分12分)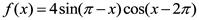 已知函数
已知函数 ,
,
(1)求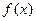 的最小正周期;
的最小正周期;
(2)若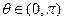 ,
,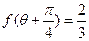 , 求
, 求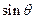 的值.
的值.
已知函数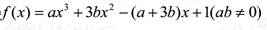 在x=1处取得极值,在x=2处的切线平行于向量
在x=1处取得极值,在x=2处的切线平行于向量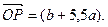
(1)求a,b的值,并求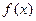 的单调区间;
的单调区间;
(2)是否存在正整数m,使得方程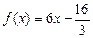 在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
在区间(m,m+1)内有且只有两个不等实根?若存在,求出m的值;若不存在,说明理由.
已知函数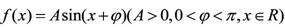 的最大值是2,
的最大值是2, 其图象经过点
其图象经过点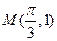 .
.
(1)求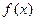 的解析式;
的解析式;
(2)已知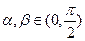 ,且
,且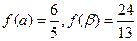 ,
,
求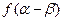 的值.
的值.