(本小题满分14分)
从某学校高一年级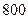 名学生中随机抽取
名学生中随机抽取 名测量身高,据测量被抽取的学生的身高全部介于
名测量身高,据测量被抽取的学生的身高全部介于 和
和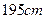 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组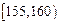 .第二组
.第二组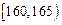 ;…第八组
;…第八组 ,右图
,右图
是按上述分组方法得到的条形图. 

(1)根据已知条件填写下面表格:
| 组 别 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 样本数 |
|
|
|
 |
|
|
|
|
(2)估计这所学校高一年级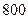 名学生中身高在
名学生中身高在 以上(含
以上(含 )的人数;
)的人数;
(3)在样本中,若第二组有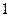 人为男生,其余为女生,第七组有
人为男生,其余为女生,第七组有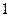 人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
人为女生,其余为男生,在第二组和第七组中各选一名同学组成实验小组,问:实验小组中恰为一男一女的概率是多少?
(本小题满分12分)
一缉私艇A发现在北偏东 方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南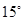 方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东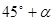 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和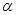 角的正弦值.
角的正弦值.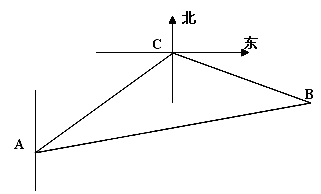
(本小题满分12分)
在 中,
中,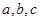 分别是角A、B、C的对边,且
分别是角A、B、C的对边,且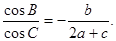
(1)求角B的大小;
(2)若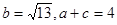 ,求
,求 的面积.
的面积.
已知数列{an}的前n项和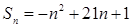 ,
,
(1)求数列{an}的通项公式;
(2)求前n项和 的最大值,并求出相应的
的最大值,并求出相应的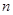 的值.
的值.
(本小题满分12分)
在△ABC中,已知 ,c=1,
,c=1,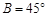 ,求A ,C, a.
,求A ,C, a.
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,
(1)求 的解析式;
的解析式;
(2)是否存在负实数 ,使得当
,使得当 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(3)对 如果函数
如果函数 的图像在函数
的图像在函数 的图像的下方,则称函数
的图像的下方,则称函数 在D上被函数
在D上被函数 覆盖.求证:若
覆盖.求证:若 时,函数
时,函数 在区间
在区间 上被函数
上被函数 覆盖.
覆盖.