如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.
(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.
(1)计算: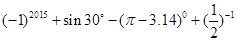 ;
;
(2)解分式方程: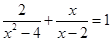 .
.
(本题满分7分,第(1)题3分,第(2)题4分)
(1)计算: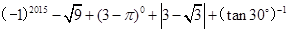
(2)解方程组: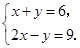
(·辽宁锦州)如图,在平面直角坐标系中,抛物线 经过点A(﹣1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.
经过点A(﹣1,0)和点B(4,0),且与y轴交于点C,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点,连接CA,CD,PD,PB.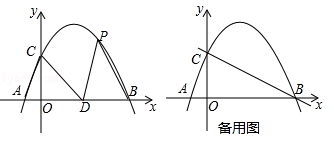
(1)求该抛物线的解析式;
(2)当△PDB的面积等于△CAD的面积时,求点P的坐标;
(3)当m>0,n>0时,过点P作直线PE⊥y轴于点E交直线BC于点F,过点F作FG⊥x轴于点G,连接EG,请直接写出随着点P的运动,线段EG的最小值.
(·辽宁锦州)如图①,∠QPN的顶点P在正方形ABCD两条对角线的交点处,∠QPN=α,将∠QPN绕点P旋转,旋转过程中∠QPN的两边分别与正方形ABCD的边AD和CD交于点E和点F(点F与点C,D不重合).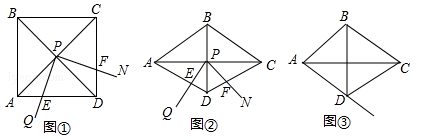
(1)如图①,当α=90°时,DE,DF,AD之间满足的数量关系是 ;
(2)如图②,将图①中的正方形ABCD改为∠ADC=120°的菱形,其他条件不变,当α=60°时,(1)中的结论变为DE+DF=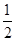 AD,请给出证明;
AD,请给出证明;
(3)在(2)的条件下,若旋转过程中∠QPN的边PQ与射线AD交于点E,其他条件不变,探究在整个运动变化过程中,DE,DF,AD之间满足的数量关系,直接写出结论,不用加以证明.
(·辽宁锦州)开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.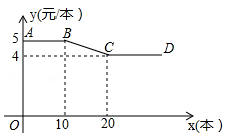
(1)图中线段AB所表示的实际意义是 ;
(2)请直接写出y与x之间的函数关系式 ;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?