（本小题满分13分）.某商品在近30天内，每件的销售价格P（元）与时间t（天）的函数关系是：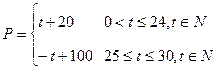
该商品的日销售量Q(件)与时间（天）的函数关系是:Q=－t+40 (0<t≤30,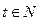
)，
求这种商品日销售金额的最大值，并指出日销售金额最大的一天是30天中的哪一天？
（文）等差数列
中，
且
成等比数列，求数列前20项的和
．
已知抛物线
的焦点为F，以点
为圆心，|AF|为半径的圆在x轴的上方与抛物线交于M、N两点。
（I）求证：点A在以M、N为焦点，且过点F的椭圆上；
（II）设点P为MN的中点，是否存在这样的a，使得|FP|是|FM|与|FN|的等差中项？如果存在，求出实数a的值；如果不存在，请说明理由。
已知函数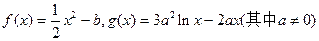
（I）求函数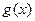
的单调递增区间；
（II）若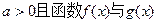
的图像有公共点，且在该点处的切线相同，用a表示b，并求b的最大值。
已知函数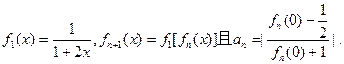
（I）求数列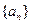
的通项公式；
（II）若数列
某学校有男教师150名，女教师100人，按照分层抽样的方法抽出5人进行一项问卷调查。
（I）求某老师被抽到的概率及5人中的男、女教师的人数；
（II）若从这5人中选出两人进行某项支教活动，则抽出的两人中恰有一名女教师的概率。