(本小题满分14分)在平面直角坐标系 中,已知直线
中,已知直线 被圆
被圆 截得的弦长为
截得的弦长为 .
.
(Ⅰ)求圆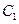 的方程;
的方程;
(Ⅱ)设圆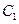 和
和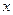 轴相交于A,B两点,点P为圆
轴相交于A,B两点,点P为圆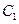 上不同于A,B的任意一点,直线
上不同于A,B的任意一点,直线 ,
,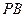 交
交 轴于M,N两点.当点P变化时,以
轴于M,N两点.当点P变化时,以 为直径的圆
为直径的圆 是否经过圆
是否经过圆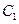 内一定点?请证明你的结论.
内一定点?请证明你的结论.
有一座大桥既是交通拥挤地段,又是事故多发地段。为了保证安全,交通部门规定,大桥上的车距y(米)与车速x(千米/小时)和车身长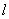 (米)的关系满足:
(米)的关系满足: ,
,
(1)求车距为2.66个车身长时的车速;
(2)假定车身长为4米,应规定怎样的车速,才能使大桥上每小时的通过的车辆最多?
(每小时通过的车辆数= )
)
如图: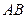 是⊙
是⊙ 的直径,
的直径, 垂直于⊙
垂直于⊙ 所在的平面,PA=AC,
所在的平面,PA=AC, 是圆周上不同于
是圆周上不同于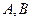 的任意一点,(1) 求证:
的任意一点,(1) 求证: 。
。
(2) 求二面角 P-BC-A的大小。
 |
(本小题满分8分)阅读下边的程序,将输出的X的值依次分别记为
(1)
|
求数列 的通项公式。
的通项公式。
(本小题满分6分)已知函数
(1)写出函数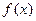 的周期;
的周期;
(2)将函数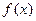 图像上所有的点向右平移
图像上所有的点向右平移 个单位,得到函数
个单位,得到函数 的图像,写出函数
的图像,写出函数 的表达式,并判断函数
的表达式,并判断函数 的奇偶性.
的奇偶性.
如图,已知圆上的弧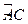 =
=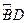 ,过C点的圆的切线与BA的延长线交于E点,证明:
,过C点的圆的切线与BA的延长线交于E点,证明: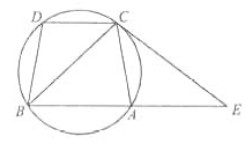
(Ⅰ)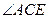 =
=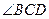 ;
;
(Ⅱ)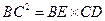 ;
;