某小型自来水厂的蓄水池中存有水400吨水,水厂每小时可向蓄水池中注入自来水60吨。若蓄水 池向居民小区不间断地供水,且
池向居民小区不间断地供水,且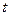 小时内供水总量为
小时内供水总量为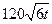 吨(
吨(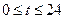 )。⑴供水开始几小时后,蓄水池中的水量最小?最小水量为多少吨?⑵若蓄水池中的水量少于80吨,就会出现供水紧张现象,试问在一天的24小时内,有多少小时会出现供水紧张现象?并说明理由。
)。⑴供水开始几小时后,蓄水池中的水量最小?最小水量为多少吨?⑵若蓄水池中的水量少于80吨,就会出现供水紧张现象,试问在一天的24小时内,有多少小时会出现供水紧张现象?并说明理由。
如图,在 中,
中,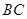 边上的中线
边上的中线 长为3,且
长为3,且 ,
,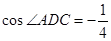 .
.
(1)求 的值;
的值;
(2)求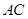 边的长.
边的长.
(本小题满分12分)f(x)=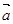 .
.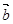 ,其中向量
,其中向量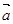 =(m,cos2x),
=(m,cos2x),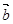 =(1+sin2x,1),
=(1+sin2x,1),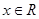 ,且函数
,且函数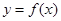 的图象经过点
的图象经过点 .
.
(Ⅰ)求实数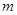 的值.
的值.
(Ⅱ)求函数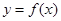 的最小值及此时
的最小值及此时 值的集合。
值的集合。
已知等差数列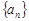 中,
中,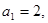
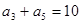 .
.
(1)求数列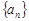 的通项公式;
的通项公式;
(2)令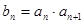 ,证明:
,证明: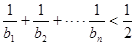 .
.
(本小题满分10分)选修4-5:不等式选讲
已知函数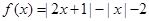 .
.
(Ⅰ)解不等式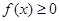 ;
;
(Ⅱ)若存在实数x,使得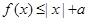 ,求实数a的取值范围.
,求实数a的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
已知在平面直角坐标系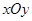 中,直线
中,直线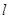 的参数方程是
的参数方程是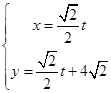 (t是参数),以原点O为极点,x轴正半轴建立极坐标系,曲线C的极坐标方程
(t是参数),以原点O为极点,x轴正半轴建立极坐标系,曲线C的极坐标方程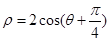 .
.
(Ⅰ)判断直线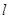 与曲线C的位置关系;
与曲线C的位置关系;
(Ⅱ)设M为曲线C上任意一点,求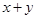 的取值范围.
的取值范围.