如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l1:x=m(|m|>1),P为l1上的动点,使∠F1PF2最大的点P记为Q,求点Q的坐标(用m表示).
(本小题满分13分)如图,在平面直角坐标系xOy中,椭圆 的离心率为
的离心率为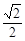 ,
,
过椭圆右焦点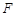 作两条互相垂直的弦AB与CD.当直线AB斜率为0时,
作两条互相垂直的弦AB与CD.当直线AB斜率为0时, .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求由A,B,C,D四点构成的四边形的面积的取值范围.
(本小题满分12分)已知等比数列{an}的公比 ,前n项和为Sn,S3=7,且
,前n项和为Sn,S3=7,且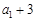 ,
,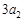 ,
,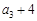
成等差数列,数列{bn}的前n项和为Tn, ,其中
,其中 N*.
N*.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求数列{bn}的通项公式;
(Ⅲ)设 ,
,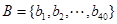 ,
, ,求集合C中所有元素之和.
,求集合C中所有元素之和.
(本小题满分12分)如图1,平面四边形ABCD关于直线AC对称,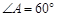 ,
, ,
, ,把△ABD沿BD折起(如图2),使二面角
,把△ABD沿BD折起(如图2),使二面角 为直二面角.如图2,
为直二面角.如图2,
(Ⅰ)求AD与平面ABC所成的角的余弦值;
(Ⅱ)求二面角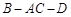 的大小的正弦值.
的大小的正弦值.
(本小题满分12分)有一种密码,明文是由三个字符组成,密码是由明文对应的五个数字组成,编码规则如下表:明文由表中每一排取一个字符组成,且第一排取的字符放在第一位,第二排取的字符放在第二位,第三排取的字符放在第三位,对应的密码由明文对应的数字按相同的次序排成一组
组成.
| 第一排 |
明文字符 |
A |
B |
C |
D |
| 密码字符 |
11 |
12 |
13 |
14 |
|
| 第二排 |
明文字符 |
E |
F |
G |
H |
| 密码字符 |
21 |
22 |
23 |
24 |
|
| 第三排 |
明文字符 |
M |
N |
P |
Q |
| 密码字符 |
1 |
2 |
3 |
4 |
设随机变量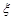 表示密码中所含不同数字的个数.
表示密码中所含不同数字的个数.
(Ⅰ)求 ;
;
(Ⅱ)求随机变量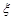 的分布列和它的数学期望.
的分布列和它的数学期望.
(本小题满分12分)已知△ABC的三内角A, B, C所对边的长依次为a,b,c,若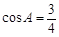 ,
, .
.
(Ⅰ)求 ;
;
(Ⅱ)若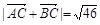 ,求△ABC的面积.
,求△ABC的面积.