一个口袋中有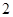 个白球和
个白球和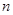 个红球(
个红球(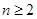 ,且
,且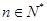 ),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
),每次从袋中摸出两个球(每次摸球后把这两个球放回袋中),若摸出的两个球颜色相同为中奖,否则为不中奖.
(1)试用含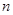 的代数式表示一次摸球中奖的概率
的代数式表示一次摸球中奖的概率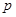 ;
;
(2)若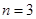 ,求三次摸球恰有一次中奖的概率;
,求三次摸球恰有一次中奖的概率;
(3)记三次摸球恰有一次中奖的概率为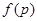 ,当
,当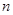 为何值时,
为何值时,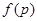 取最大值.
取最大值.
已知等差数列{ }中
}中 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
设正项等差数列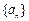 的前n项和为
的前n项和为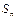 ,其中
,其中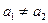 .
. 是数列
是数列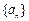 中满足
中满足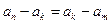 的任意项.
的任意项.
(1)求证: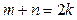 ;
;
(2)若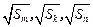 也成等差数列,且
也成等差数列,且 ,求数列
,求数列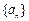 的通项公式;
的通项公式;
(3)求证: .
.
 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形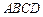 和
和 构成的面积为200
构成的面积为200 的十字型地域,计划在正方形
的十字型地域,计划在正方形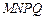 上建一座“观景花坛”,造价为4200元
上建一座“观景花坛”,造价为4200元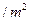 ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元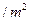 ,再在四个空角(如
,再在四个空角(如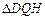 等)上铺草坪,造价为80元
等)上铺草坪,造价为80元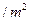 .设
.设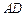 长为
长为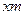 ,
, 长为
长为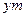 .
.
(1)试找出 与
与 满足的等量关系式;
满足的等量关系式;
(2)设总造价为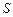 元,试建立
元,试建立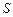 与
与 的函数关系;
的函数关系;
(3)若总造价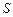 不超过138000元,求
不超过138000元,求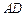 长
长 的取值范围.
的取值范围.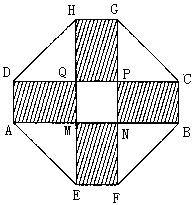
已知数列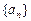 满足:
满足: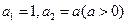 ,数列
,数列 满足
满足 .
.
(1)若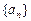 是等差数列,且
是等差数列,且 求
求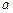 的值及
的值及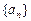 的通项公式;
的通项公式;
(2)若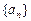 是等比数列,求
是等比数列,求 的前
的前 项和
项和 ;
;
(3)若 是公比为
是公比为 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数 ,使得数列
,使得数列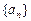 为等比数列?若存在,求出
为等比数列?若存在,求出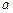 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
在平面直角坐标系 中,点
中,点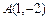 ,
,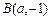 ,
,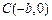 ,且
,且 .
.
(1)若点 、
、 、
、 在直线
在直线 上,求
上,求
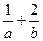 的最小值,并求此时直线
的最小值,并求此时直线 的方程;
的方程;
(2)若以线段 、
、 为邻边的平行四边形两条对角线的长相等,且
为邻边的平行四边形两条对角线的长相等,且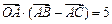 ,求
,求 、
、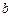 的值.
的值.