已知椭圆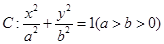
的短半轴长为
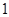，动点
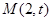
在直线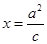
（
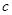为半焦距）上．
（1）求椭圆的标准方程；
（2）求以
为直径且被直线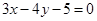
截得的弦长为
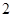的圆的方程；
（3）设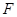
是椭圆的右焦点，过点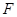作的垂线与以为直径的圆交于点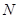
，
求证：线段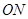
的长为定值，并求出这个定值．
如图，AB是⊙O的直径，C、F是⊙O上的点，AC是∠BAF的平分线，过点C作CD⊥AF，交AF的延长线于点D．
（1）求证：CD是⊙O的切线．
（2）过C点作CM⊥AB，垂足为M，求证：AM•MB=DF•DA．
已知函数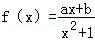
在点（﹣1，f（﹣1））的切线方程为x+y+3=0．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）设g（x）=lnx，求证：g（x）≥f（x）在x∈[1，+∞）上恒成立．
如图，已知菱形ACSB中，∠ABS=60°．沿着对角线SA将菱形ACSB折成三棱锥S﹣ABC，且在三棱锥S﹣ABC中，∠BAC=90°，O为BC中点．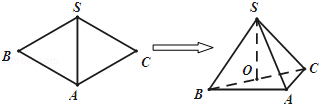
（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）求平面ASC与平面SCB夹角的余弦值．
在梯形ABCD中，AD∥BC，BC=2AD，AD=AB=
，AB⊥BC，如图把△ABD沿BD翻折，使得平面ABD⊥平面BCD．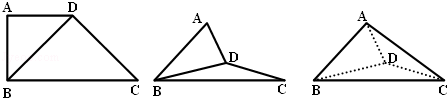
（Ⅰ）求证：CD⊥平面ABD；
（Ⅱ）若点M为线段BC中点，求点M到平面ACD的距离．
已知{an}是正项数列，a1=1，且点（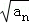
，an+1）（n∈N*）在函数y=x2+1的图象上．
（1）求数列{an}的通项公式；
（2）若列数{bn}满足b1=1，bn+1=bn+2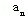
，求证：bnbn+2＜b
．