已知{an}是正项数列,a1=1,且点(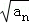 ,an+1)(n∈N*)在函数y=x2+1的图象上.
,an+1)(n∈N*)在函数y=x2+1的图象上.
(1)求数列{an}的通项公式;
(2)若列数{bn}满足b1=1,bn+1=bn+2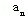 ,求证:bnbn+2<b
,求证:bnbn+2<b .
.
已知点P(0,5)及圆C:x2+y2+4x-12y+24=0
(I)若直线l过点P且被圆C截得的线段长为4 ,求l的方程;
,求l的方程;
(II)求过P点的圆C的弦的中点D的轨迹方程
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥面ABC,D、E分别是棱A1B1、AA1的中点,点F在棱AB上,且

(I)求证:EF∥平面BDC1;
(II)求二面角E-BC1-D的余弦值
已知函数 ,
,
(I)若 ,求函数
,求函数 的最大值和最小值,并写出相应的x的值;
的最大值和最小值,并写出相应的x的值;
(II)设 的内角
的内角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,满足
,满足 ,
, 且
且 ,求
,求 、
、 的值
的值
已知:等差数列{an}中,a3+a4=15,a2a5=54,公差d<0.
(I)求数列{an}的通项公式an;
(II)求数列的前n项和Sn的最大值及相应的n的值.
已知等比数列 的公比为
的公比为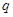 ,
, 是
是 的前
的前 项和.
项和.
(1)若 ,
,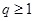 ,求
,求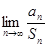 的值;
的值;
(2)若 ,
,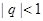 ,
, 有无最值?并说明理由;
有无最值?并说明理由;
(3)设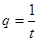 ,若首项
,若首项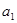 和
和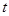 都是正整数,
都是正整数,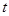 满足不等式:
满足不等式: ,且对于任意正整数
,且对于任意正整数 有
有 成立,问:这样的数列
成立,问:这样的数列 有几个?
有几个?