已知函数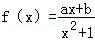 在点(﹣1,f(﹣1))的切线方程为x+y+3=0.
在点(﹣1,f(﹣1))的切线方程为x+y+3=0.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)=lnx,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立.
已知函数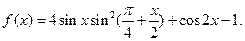
(1)设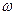 >0为常数,若
>0为常数,若 上是增函数,求
上是增函数,求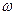 的取值范围;
的取值范围;
(2)设集合 若A
若A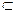 B恒成立,求实数
B恒成立,求实数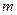 的取值范围
的取值范围
已知圆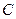 过点
过点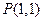 且与圆M:
且与圆M: 关于直线
关于直线 对称
对称
(1)判断圆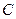 与圆M的位置关系,并说明理由;
与圆M的位置关系,并说明理由;
(2)过点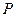 作两条相异直线分别与圆
作两条相异直线分别与圆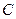 相交于
相交于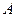 、
、
①若直线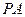 与直线
与直线 互相垂直,求
互相垂直,求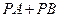 的最大值;
的最大值;
②若直线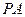 与直线
与直线 与
与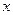 轴分别交于
轴分别交于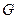 、
、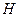 ,且
,且 ,
,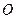 为坐标原点,试判断直线
为坐标原点,试判断直线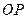 与
与 是否平行?请说明理由.
是否平行?请说明理由.
直线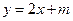 和圆
和圆 交于
交于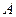 、B两点,以为
、B两点,以为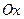 始边,
始边,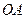 、
、 为终边的角分别为
为终边的角分别为 、
、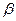 ,求
,求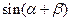 的值
的值
设向量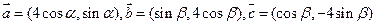

(1)若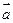 与
与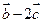 垂直,求
垂直,求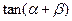 的值;
的值;
(2)求 的最大值;
的最大值;
(3)若 ,求证:
,求证: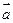 ∥
∥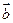 .
.
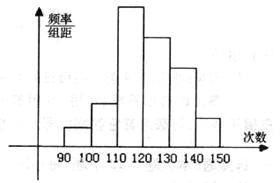
为了了解高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
(1)求第二小组的频率;
(2)求样本容量;
(3)若次数在110以上为达标,试估计全体高一学生的达标率为多少?