如图,AB是⊙O的直径,C、F是⊙O上的点,AC是∠BAF的平分线,过点C作CD⊥AF,交AF的延长线于点D.
(1)求证:CD是⊙O的切线.
(2)过C点作CM⊥AB,垂足为M,求证:AM•MB=DF•DA.
(本小题满分14分)已知函数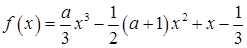 (
(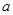
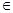 R).
R).
(1)若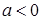 ,求函数
,求函数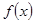 的极值;
的极值;
(2)是否存在实数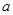 使得函数
使得函数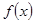 在区间
在区间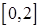 上有两个零点,若存在,求出
上有两个零点,若存在,求出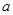 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
(本小题满分13分)
(本小题满分12分)某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为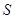 平方米.
平方米.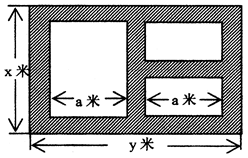
(1)分别写出用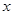 表示
表示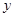 和用
和用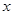 表示
表示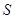 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
(本小题满分12分)如图,棱柱ABCD—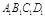 的底面
的底面 为菱 形 ,AC∩BD=O侧棱
为菱 形 ,AC∩BD=O侧棱 ⊥BD,点F为
⊥BD,点F为 的中点.
的中点.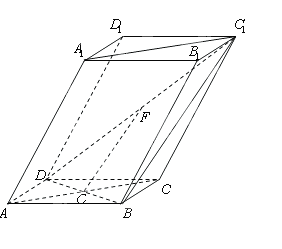
(Ⅰ)证明: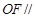 平面
平面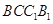 ;
;
(Ⅱ)证明:平面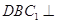 平面
平面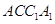 .
.
(本小题满分12分)已知数列 是等差数列,
是等差数列,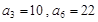 ,数列
,数列 的前n项和是
的前n项和是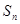 ,且
,且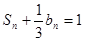 .
.
(I)求数列 的通项公式;
的通项公式;
(II)求证:数列 是等比数列;
是等比数列;
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2个小题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系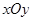 中,把矩阵
中,把矩阵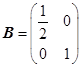 确定的压缩变换
确定的压缩变换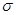 与矩阵
与矩阵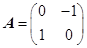 确定的旋转变换
确定的旋转变换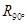 进行复合,得到复合变换
进行复合,得到复合变换 .
.
(Ⅰ)求复合变换 的坐标变换公式;
的坐标变换公式;
(Ⅱ)求圆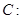
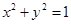 在复合变换
在复合变换 的作用下所得曲线
的作用下所得曲线 的方程.
的方程.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系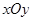 中,直线
中,直线 的参数方程为
的参数方程为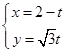 (
( 为参数),
为参数),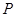 、
、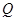 分别为直线
分别为直线 与
与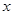 轴、
轴、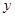 轴的交点,线段
轴的交点,线段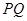 的中点为
的中点为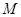 .
.
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点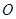 为极点,
为极点,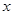 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点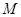 的极坐标和直线
的极坐标和直线 的极坐标方程.
的极坐标方程.
(3)(本小题满分7分)选修4—5:不等式选讲
已知不等式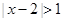 的解集与关于
的解集与关于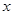 的不等式
的不等式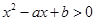 的解集相等.
的解集相等.
(Ⅰ)求实数 ,
,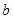 的值;
的值;
(Ⅱ)求函数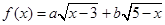 的最大值,以及取得最大值时
的最大值,以及取得最大值时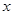 的值.
的值.