(本小题8分)已知函数 ,
, ,其中
,其中 .
.
(1)设函数 .若
.若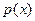 在(0,3)上有零点,求
在(0,3)上有零点,求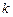 的取值范围;
的取值范围;
(2)设函数 是否存在
是否存在 ,对任意给定的非零实数
,对任意给定的非零实数 ,存在惟一的非零实数
,存在惟一的非零实数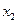 (
(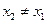 ),使得
),使得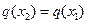 ?若存在,求
?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知向量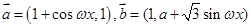 (
(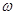 为常数且
为常数且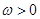 ),函数
),函数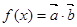 在
在 上的最大值为
上的最大值为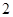 .
.
(1)求实数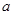 的值;
的值;
(2)把函数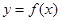 的图象向右平移
的图象向右平移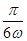 个单位,可得函数
个单位,可得函数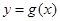 的图象,若
的图象,若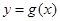 在
在 上为增函数,求
上为增函数,求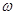 取最大值时的单调增区间.
取最大值时的单调增区间.
已知椭圆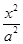 +
+ =1(a>b>0)的左、右焦点分别为F1、F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=
=1(a>b>0)的左、右焦点分别为F1、F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=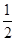
(1)求椭圆的标准方程;
(2)若P是椭圆上的任意一点,求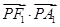 的取值范围;
的取值范围;
(3)已知直线l:y=kx+m与椭圆相交于不同的两点M,N(均不是长轴的端点),AH⊥MN,垂足为H且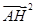 =
= ,求证:直线l恒过定点.
,求证:直线l恒过定点.
已知向量a=(cosα,sinα),b=(cosβ,sinβ),c=(-1,0).
(1)求向量b+c的长度的最大值;
(2)设α=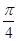 ,且a⊥(b+c),求cosβ的值.
,且a⊥(b+c),求cosβ的值.
已知函数 ,
, ,
, .
.
(1)若当 时,恒有
时,恒有 ,求
,求 的最大值;
的最大值;
(2)若当 时,恒有
时,恒有 ,求
,求 的取值范围.
的取值范围.
(设函数f(x)=|x+a|-|x-4|,x R
R
(1)当a=1时,解不等式f(x)<2;
(2)若关于x的不等式f(x)≤5-|a+l|恒成立,求实数a的取值范围.